Seja

1. Determine os pontos críticos de e classifique-os.
2. Determine o máximo e o mínimo de no quadrado (com interior e bordas) cujos vértices são , , e .

Show! Agora vamos zerar as derivadas parciais:

Obtivemos um sistema que basicamente vai ser uma equação de segundo grau, saca só:

ou

Logo, os pontos críticos da são: e .

Por enquanto tá sussa né? Vamos continuar!

Já fizemos a primeira parte da questão, achamos os pontos críticos. Agora temos que classificá-los, usando o teste da derivada segunda. Lembrando que temos:

e

Vamos calcular as derivadas segundas:

E com a regra do produto:

Agora, pras derivadas mistas vamos ter:

Agora podemos aplicar o teste da derivada segunda pros dois pontos críticos. Vamos começar com o ponto :

Logo, o ponto é ponto de sela.

Vamos dar uma olhada agora no ponto :

Além disso:

Então o ponto é um ponto de mínimo local.

b) Nós queremos os pontos de máximo e mínimo da no quadrado. Vamos examinar os possíveis candidatos, analisando o interior e a borda do quadrado.

No interior do quadrado, temos um candidato a mínimo, que é ponto , um ponto crítico da , como vimos na questão anterior.

Podemos notar também que os vértices do quadrado são candidatos a máximo e mínimo, pois eles são os extremos da região. Isso nos dá mais 4 candidatos: os pontos , , e .

Observação: o ponto é, inclusive, um ponto crítico da , como vimos na letra a).

Vamos analisar agora os lados do quadrado um por um. Repare que vamos sempre ter uma coordenada variando de 0 a 3 enquanto outra fica fixada. Ou seja, na borda do quadrado a só depende de uma variável.

Por isso, pra facilitar nossa conta, vamos criar uma função de uma variável para cada lado e determinar os pontos críticos dessas funções. Esses pontos críticos também vão ser candidatos a máximo ou mínimo da no quadrado. Ficou confuso? Relaxa que não é tão complicado, dá uma olhada:

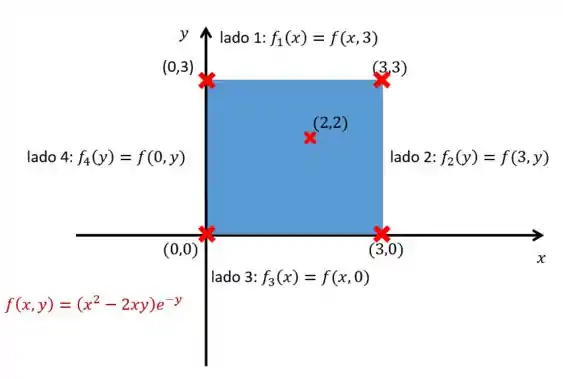
Lado 1: e

ou

Logo, não tem nenhum ponto crítico em .

Lado 2: e

Opa! Achamos um ponto crítico! O ponto .

Lado 3: e

Nada de ponto crítico pra em , então vamos pro lado 4!

Lado 4: Nem precisamos usar a , pois a se anula no lado 4 todo, porque e

Opa, então podemos substituir os candidatos e que tínhamos por , com

Show! Agora já temos todos os nossos pontos candidatos a máximo ou mínimo da no quadrado:

Agora só nos resta determinar qual ponto é o máximo e qual é o mínimo. Basta calcular o valor da função nesses pontos:

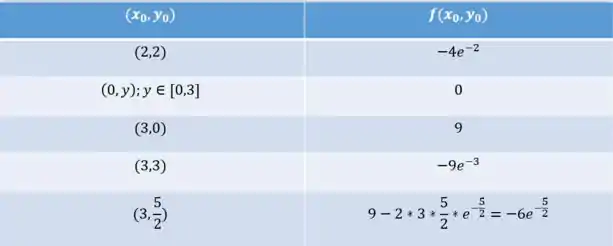
O máximo é pois esse é o único valor positivo. Já o mínimo não é tão fácil de determinar, só tem valor estranho com exponencial: ; e . O valor que tiver o maior módulo vai ser o mais distante de 0 e, portanto, o mínimo de .

Então pra resolver isso vamos começar pegando dois valores e fazendo a razão deles. Se der maior do que 1, o numerador tem maior módulo, se der menor que 1, o denominador que tem o maior módulo. Que tal?

Ou seja:

Vamos testar o agora:

Ih! E agora? Isso dá mais ou menos que 1? Calma, só tem três possibilidades:

ou

ou

Mas podemos ver que a opção é a certa, olha só:

Logo,

Portanto, o mínimo da função no quadrado vale e é atingido no ponto , e o máximo é , no ponto .