Os valores máximo e mínimo absolutos de
Na região
São, respectivamente
Passo 1
Primeiramente, vamos identificar que região é essa.
Ela é limitada pelas retas
Graficamente, temos esse triângulo limitado pelas retas azul, rosa e vermelha, respectivamente:
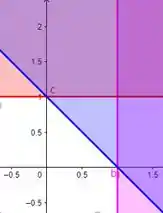
Então, teremos que buscar os candidatos a máximo e mínimo da nossa função dentro do triângulo e na fronteira dele.
Passo 2
Verificando os pontos críticos dentro da região:
Igualando a zero:
Isso significa que não temos candidatos a máximo e mínimo no interior da nossa região.
Passo 3
Antes de passar pra fronteira da região, precisamos guardar os vértices do triângulo que é a nossa região.
São os pontos:
Portanto, temos 3 pontos candidatos a máximo e mínimo.
Passo 4
Vamos para a fronteira agora.
Vamos dividir nossa fronteira em 3:
•Lado 1:
• Lado 2:
•Lado 3:
Em cada lado a função só depende de uma variável, e nós temos que achar os pontos críticos dessas 3 “subfunções”.
Passo 5
Comecemos pelo lado . Lembrando a nossa função:
E o primeiro lado:
Substituindo o lado na função:
Temos que achar o valor de máximo dessa função, vamos derivar e igualar a zero. Neste caso derivamos em relação a
Opa, isso aí não rola ne? Então não temos candidatos sobre o lado 1.
Passo 6
Agora precisamos fazer o mesmo pro segundo lado :
Substituindo esse lado na função, teremos:
Desenvolvendo,
Temos que achar os pontos críticos dessa função, vamos derivar e igualar a zero. Neste caso derivamos em relação a
Também não rola, né? Então também não temos candidatos sobre o lado 2.
Passo 7
Vamos verificar para o terceiro e último lado :
Substituindo-o na função:
Desenvolvendo,
Neste caso derivamos em relação a
Assim, obtemos o ponto . Mas ele nós já consideramos, é um vértice do triângulo!
Então o lado 3 também não acrescentou nada novo.
Passo 8
Ok, agora já temos todo o material necessário para terminar de vez com isso e dizer quais são os pontos de máximo e mínimo!
Os nossos candidatos são os pontos:
Passo 9
Só nos resta calcular o valor da função em cada ponto. Lembrando que
Então temos
Show, então os ponto de mínimo global e máximo global de são, respectivamente, e .
O valor mínimo é e o valor máximo é .
Resposta
Letra