Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Máximos e Mínimos Globais numa Região Fechada

Ver Teoria
Exercício 37123456789101112131415161718192021222324252627282930313233343536383940414243444546

Enunciado

UFABC. Cálculo. Funções de Várias Variáveis. Lista 5 - Pontos Críticos, Máximos e Mínimos, Multiplicadores de Lagrange. Questão 2c.

2 - Encontre o máximo e mínimo globais de cada uma das seguintes funções:

c) f x , y = e x 2 + y 2 + y , x ≤ 1 , y ≤ 1 .

Passo 1

Iae, como vai? Essa questão está um pouco complicada? Fique tranquilo que vamos tentar te ajudar. 😎👍

Para resolver esse probleminha, vamos ter que encontrar o ponto onde f assume o maior valor e o ponto onde f assume o menor valor.

Tem um porém, temos que achar esses pontos dentro do espaço limitado por x ≤ 1 e y ≤ 1 . Vamos dar uma olhada como é este espaço?

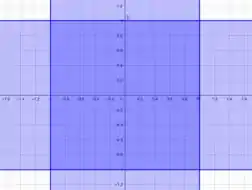
Este espaço representa um quadrado limitado pelar retas x = - 1 , x = 1 , y = - 1 e y = 1 .

Para calcular esses pontos, vamos calcular os pontos críticos pelo método convencional e ignorar os pontos situados fora da nossa área. Além disso, temos que calcular os pontos de máximos e mínimos em cada borda da nossa área.

Mas vamos com calma, primeiro vamos obter os pontos pelo método convencional.

Bora lá!

Passo 2

Pelo método convencional, vamos derivar f em função de x e y , igualar as duas derivadas a 0 , assim vamos obter um sistema de equações, as soluções serão os candidatos às coordenadas dos pontos críticos.

f x = ∂ e x 2 + y 2 + y ∂ x

Para essa derivada, vamos usar a regra da cadeia, onde k = x 2 + y 2 + y

∂ e x 2 + y 2 + y ∂ x = ∂ x 2 + y 2 + y ∂ x · ∂ e k ∂ k

f x = 2 x e k

Substituindo k = x 2 + y 2 + y , temos

f x = 2 x e x 2 + y 2 + y

Vamos calcular f y

f y = ∂ e x 2 + y 2 + y ∂ y

Novamente vamos derivar a partir da regra da cadeia, onde h = x 2 + y 2 + y

∂ e x 2 + y 2 + y ∂ y = ∂ x 2 + y 2 + y ∂ y · ∂ e h ∂ h

f y = 2 y + 1 e h

Substituindo h = x 2 + y 2 + y

f y = 2 y + 1 e x 2 + y 2 + y

Igualando a 0 , obtemos o sistema

2 x e x 2 + y 2 + y = 0 2 y + 1 e x 2 + y 2 + y = 0

Bora calcular a solução desse sistema?

Passo 3

Analisando nosso sisteminha, vemos que e x 2 + y 2 + y nunca será igual a 0 , então para satisfazer a equação, temos

2 x = 0 2 y + 1 = 0

Logo encontramos

x = 0 y = - 1 2

Encontramos nosso primeiro ponto P 1 = 0 , - 1 2 .

Agora vamos usar o método não convencional. Precisamos saber se nas bordas da área, tem algum ponto de máximo ou ponto de mínimo.

Pra isso, vamos substituir as retas na função e ver seu comportamento. Por exemplo

Para a borda limitada por x = - 1

f - 1 , y = e - 1 2 + y 2 + y

f y = e 1 + y 2 + y

Nesse caso vamos usar o método convencional para obter o ponto que queremos

f - 1 , y = ∂ e 1 + y 2 + y ∂ y

Pela regra da cadeia, vemos que

f - 1 , y = 2 y + 1 e 1 + y 2 + y

Com isso, obtemos

2 y + 1 e 1 + y 2 + y = 0

Já vimos a solução de algo parecido 🤔

Se e 1 + y 2 + y nunca vai a 0 , só resta 2 y + 1 ser igual a 0 , logo

2 y + 1 = 0

y = - 1 2

Com isso, obtemos o ponto P 2 = - 1 , - 1 2 .

Entendeu?

Passo 4

Para a borda limitada por x = 1

f 1 , y = e 1 2 + y 2 + y

f y = e 1 + y 2 + y

Essa foi a função que acabamos de calcular, não foi? Então a solução será a mesma.

Dessa forma, obtemos mais um ponto sem muito esforço P 3 = 1 , - 1 2 .

Para a borda limitada por y = - 1

f x , - 1 = e x 2 + - 1 2 + - 1

f x = e x 2

Vamos obter a solução de f x , - 1 = 0

f x , - 1 = ∂ e x 2 ∂ x

Pela regra da cadeia nossa derivada será

f x , - 1 = 2 x e x 2

Com isso, temos

2 x e x 2 = 0

Como e x 2 nunca vai a 0 , esse papel sobrou para o 2 x , logo

2 x = 0 → x = 0

Assim, obtemos mais um ponto P 4 = 0 , - 1 .

Bacana, não é?

Passo 5

Por fim, para a borda y = 1

f x , 1 = e x 2 + 1 2 + 1

f x = e x 2 + 2

Calculando a solução de f x , 1 = 0 , temos

f x , 1 = ∂ e x 2 + 2 ∂ x

Pela regra da cadeia, temos

f x , 1 = 2 x e x 2 + 2

2 x e x 2 + 2 = 0

Novamente e x 2 + 2 não consegue ser 0 , então x = 0 .

Com isso, encontramos mais um pontinho P 5 = 0,1 .

Vemos que não obtemos nenhum vértice da nossa área, então devemos considera-los.

P 6 = 1,1 , P 7 = - 1,1 , P 8 = 1 , - 1 e P 9 = - 1 , - 1 .

Não se esqueça dessa parte, é muito importante: “Quando não encontramos os vértices da nossa área no cálculo das bordas, devemos considera-las como possíveis pontos de máximos ou mínimos!”

Passo 6

Depois de todos os pontos calculados, vamos ver o valor de f para cada um deles e selecionar o maior valor e o menor valor como resultado.

Lembrando que

f x , y = e x 2 + y 2 + y

Para o ponto P 1 = 0 , - 1 2 , temos

f 0 , - 1 2 = e 0 2 + - 1 2 2 + 1 2

f 0 , - 1 2 = e - 1 4

Para o ponto P 2 = - 1 , - 1 2

f - 1 , - 1 2 = e - 1 2 + - 1 2 2 + 1 2

f - 1 , - 1 2 = e 3 4

Para o ponto P 3 = 1 , - 1 2

f 1 , - 1 2 = e 1 2 + - 1 2 2 + 1 2

f 1 , - 1 2 = e 3 4

Para o ponto P 4 = 0 , - 1

f 0 , - 1 = e 0 2 + - 1 2 + - 1

f 0 , - 1 = 1

Para o ponto P 5 = 0,1

f 0,1 = e 0 2 + 1 2 + 1

f 0,1 = e 2

Agora vamos calcular os vértices da nossa área

Passo 7

Para o ponto P 6 = 1,1

f 1,1 = e 1 2 + 1 2 + 1

f 1,1 = e 3

Para o ponto P 7 = - 1,1

f - 1,1 = e - 1 2 + 1 2 + 1

f - 1,1 = e 3

Para o ponto P 8 = 1 , - 1

f 1 , - 1 = e 1 2 + - 1 2 + - 1

f 1 , - 1 = e 1

Por fim, para o ponto P 9 = - 1 , - 1

f - 1 , - 1 = e - 1 2 + - 1 2 + - 1

f - 1 , - 1 = e 1

Agora, apenas comparando os resultados de f , vemos que para o ponto P 7 = - 1,1 e P 6 = 1,1 , a função atingiu seu maior valor, ou seja, - 1,1 e 1,1 são nossos máximos globais!

Já o ponto P 1 = 0 , - 1 2 obteve o menor valor de f , portanto ele será nosso mínimo global!

E todos viveram felizes para sempre. Fim! 😉 Entendeu tudo? Responde Aí

Resposta

- 1,1 e 1,1 : Máximos globais.

0 , - 1 2 : Mínimo global.

Exercícios de Livros Relacionados

Entre todos os triângulos de perímetro igual a 10 cm, encontrar o que tem maior área
Encontre três números positivos que a soma é 12 e a soma dos seus quadrados é a menos possível.
Encontre as dimensões da caixa com volume 1000 cm³ que tem a menor área de superfície.
Dada a função z = a x 2 + b y 2 + c , analisar os pontos críticos, considerando que:a) a0 e b0 .
Encontre as dimensões do quadrado retangular com o maior volume se a área da superfície total é dada por 64 cm².