Determine os pontos de máximo e de mínimo globais da função restrita à elipse
Passo 1
Se você conseguir plotar essa função, a gente não precisa nem fazer conta direito pra ver os pontos de máximo e mínimo. Observa que temos uma superfície plana
Restrita dentro da elipse .
Isso nos da:
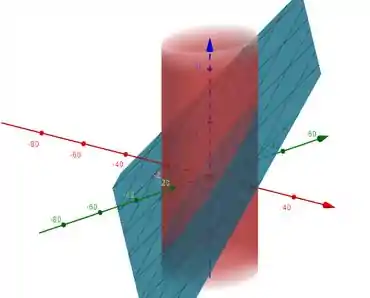
Tendo isso em mente conseguimos observar que os pontos de máximo e mínimo vão estar nos estremos da elipse (9,16) e (-9,-16) (que são os valores nos denominadores da elipse).
Tranquilo demais, né??
Passo 2
Resposta
Exercícios de Livros Relacionados
Entre todos os triângulos de perímetro igual a 10 cm, encontrar o que tem maior área
Encontre três números positivos que a soma é 12 e a soma dos seus quadrados é a menos possível.
Encontre as dimensões da caixa com volume 1000 cm³ que tem a menor área de superfície.
Dada a função z = a x 2 + b y 2 + c , analisar os pontos críticos, considerando que:a) a0 e b0 .
Encontre as dimensões do quadrado retangular com o maior volume se a área da superfície total é dada por 64 cm².