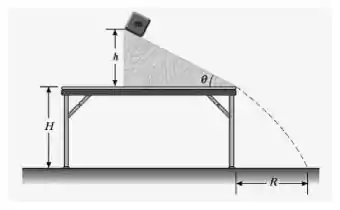
Um bloco de massa é solto do repouso a acima da superfície de uma mesa, no topo de um plano inclinado com , conforme mostrado na figura. O plano inclinado é fixado sobre uma mesa de altura .
- Determine a aceleração do bloco enquanto ele desce escorregando pelo plano inclinado.
- Qual é a velocidade escalar do bloco quando ele deixa o plano inclinado?
- A que distância da mesa o bloco atingirá o solo?
- Quanto tempo leva entre o bloco ser solto e o instante em que atinge o solo?
- A massa do bloco afeta algum dos cálculos precedentes?
Passo 1
E aiii galera, tudo bem? Essa questão é cheia de etapas, mas vou fazer passo a passo com você!
Vem comigo!

Letra a):
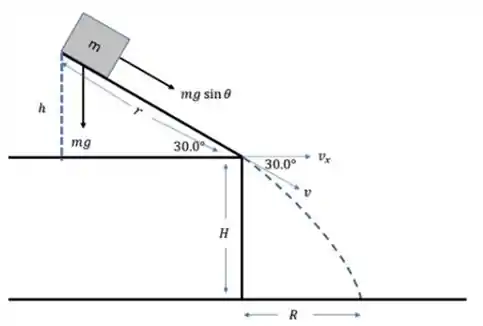 Aplicando a segunda lei de Newton ao bloco quando ele está inclinado.
Aplicando a segunda lei de Newton ao bloco quando ele está inclinado.
Olhando para a parte do bloco no plano. A única força que faz ele se movimentar é a componente ao longo do plano da força peso, então:
Aí a aceleração que ele desce é:
É essa a aceleração com que o bloco desce!
Beleza? Vamos para o próximo item?
Passo 2
Letra b):
O bloco parte do repouso e desce uma altura , então ganha energia cinética! E por conservação de energia podemos calcular a velocidade com que o bloco chega no fim do bloco:
Passo 3
Letra d): vamos separar em dois tempos: o tempo para descer o plano, depois para chegar ao chão.
A partir do repouso até a velocidade de , com uma aceleração de , podemos calcular o tempo que o bloco leva para descer o plano:
Então, o tempo é:
 Esse é o tempo que o bloco leva para chegar no fim do plano! Falta calcular o tempo que ele leva para chegar no chão!
Esse é o tempo que o bloco leva para chegar no fim do plano! Falta calcular o tempo que ele leva para chegar no chão!
Quando o bloco sai da inclinação, cai como um projétil. Vamos usar a equação horária da posição para determinar o tempo que ele levou para atingir , partindo da altura :
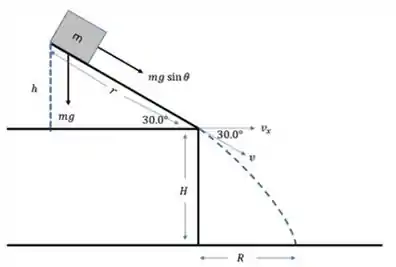
E aqui vamos ressuscitar nossa bascara!
E ignorando o resultado negativa:
Aí o tempo total é:

Passo 4
Letra c) com o tempo que o bloco leva a partir da saída do plano até a chagada no chão, podemos encontrar o alcance ! A velocidade que vamos usar aqui é a componente horizontal da velocidade
Substituindo:
Beleza? Vamos para o último item?
Passo 5
Letra e:
Podemos ver na primeira equação que a aceleração do bloco durante a descida do plano depende apenas da aceleração gravitacional e do ângulo
E enquanto há queda (vertical), sua aceleração é a aceleração gravitacional
Portanto, seu movimento não depende da massa, uma vez que a aceleração gravitacional é uma constante