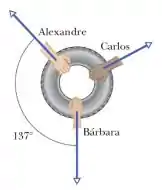
Em um cabo-de-guerra bidimensional, Alexandre, Bárbara e Carlos puxam horizontalmente um pneu de automóvel nas orientações mostradas na Figura. Apesar dos esforços da trinca, o pneu permanece no mesmo lugar. Alexandre puxa com uma força de módulo e Carlos puxa com uma força de módulo . Observe que a orientação de não é dada. Qual é o módulo da força exercida por Bárbara?
Passo 1
Oi gente, tudo bem com vocês?
É o seguinte, nessa questão temos três pessoas puxando pneu. Mas, é dito no enunciado que o pneu não sai do lugar. Ou seja, a força resultante no pneu é nula. Porém, foram dadas apenas as forças aplicadas por Alexandre e Carlos.
O enunciado quer saber justamente qual a força aplicada por Bárbara para que o pneu, de fato, esteja parado.
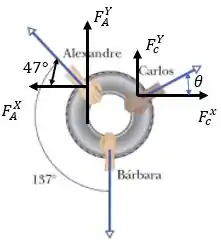
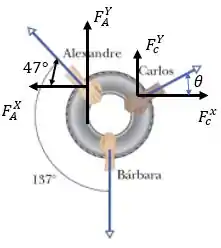
Na figura acima, decompomos as forças de Alexandre e Carlos no eixo horizontal e vertical, e colocamos também os ângulos de decomposição, sendo: para Alexandre e para Carlos.
Como o pneu está em equilíbrio, o somatório das forças na horizontal e o somatório das forças na vertical precisa ser nulo.
Assim, vamos calcular esses somatórios para encontrar o valor da força feita por Bárbara.
Passo 2
Temos:
Vamos começar escrevendo o equilíbrio de forças na direção horizontal.
Como:
Logo:
Beleza!!
Passo 3
Vamos agora verificar o equilíbrio de forças em :
Precisamos apenas determinar quanto vale o seno de pra matar a nossa questão.
Da trigonometria, temos:
Logo:
Assim:
Prontinho! Matamos mais uma 😊
Obrigado pela atenção gente!