USP, Sem Campus, Física 1, Listas de Física 1 - USP - Lista de Exercícios 1, Questão 9
Considere dois pontos localizados em posições e , de tal forma que esses pontos estão separados por uma distância . Encontre uma expressão para o vetor que vai da origem até um ponto na reta que liga a , e que está a uma distância do ponto , onde é algum número (por simplicidade, imagine ).
Passo 1
Fala, galera! Vamos resolver essa questão!
O enunciado pediu pra gente encontrar o vetor , que vai da origem até um ponto na reta que liga a , e que está a uma distância do ponto , onde é algum número. Seria isso aqui:
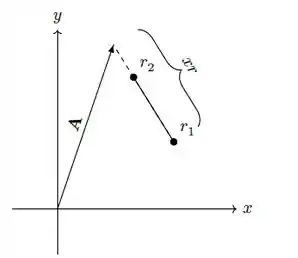
Vamos lá!
Passo 2
Observando a figura, a gente percebe que o nosso vetor vai da origem do plano até mais o seguimento que vai de a . Esse seguimento é multiplicado por um número , de modo que nós temos .
Representando matematicamente, nosso vetor será dado por:
Onde .
Valeu, galera! Até a próxima! 😉