3) Um corpo de massa está sujeito unicamente à ação de três forças constantes, e , no plano , e cujos módulos valem, respectivamente, , e . A situação está ilustrada na figura abaixo, onde o ângulo é tal que e .
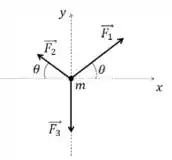
O corpo experimenta uma aceleração que, em termos dos vetores unitários e , está corretamente escrita na alternativa:
(a)
(b)
(c)
(d)
(e)
Passo 1
Fala aí, galerinha!! Esse é um problema para a gente trabalhar com decomposição de forças e a segunda lei de Newton. A história é a seguinte, temos um corpo de massa sujeito àquelas forças representadas na figura. Nós temos que encontrar o vetor aceleração desse corpo. Então a gente usa a segunda lei de Newton:
Onde é a força resultante do sistema. Então o que a gente vai fazer é primeiro encontrar essa força resultante fazendo algumas decomposições e somas vetoriais e depois usar a expressão:
Para encontrar a aceleração. Partiu??
Passo 2
O problema nos deu o seguinte diagrama de corpo livre no plano
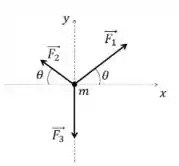
A ideia aqui é escrever cada um desses vetores na forma:
Vamos começar com Como ele só tem componente no eixo e apontando para o sentido negativo temos:
Como o enunciado nos diz que . Temos
Passo 3
Para e temos que fazer uma decomposição nos eixos a partir do ângulo A decomposição de é demonstrada nessa figura aqui
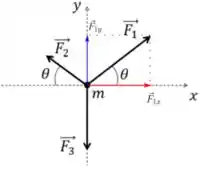
Como ambas as componentes apontam para o sentido positivo dos eixos temos:
Aqueles e são dados a partir de e o módulo através de:
Usando os valores dados no enunciado temos:
Dessa forma a decomposição nos dá:
A decomposição de é demonstrada nessa figura aqui
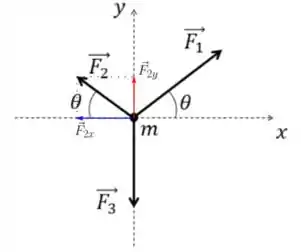
Como a componente em aponta no sentido positivo e a componente em aponta para o sentido negativo do eixo temos:
Aqueles e são dados a partir de e o módulo através de:
Usando os valores dados no enunciado temos:
Dessa forma a decomposição nos dá:
Passo 4
Agora que a gente já fez a decomposição das forças e , a força resultante é dada pela soma vetorial:
A soma vetorial é feita somando cada componente correspondente. Assim ó:
Como obtemos a força resultante e temos que o corpo tem massa usando a expressão:
Essa divisão aí a agente faz dividindo cada componente por aquele número de baixo:
E aí resolvemos essa 😊 Vamos para a próxima?
Resposta
(d)