USP, Sem Campus, Física 1, Coletânea de Exercícios - Parte II - Colisões, Torque, Cinemática Angular, Questão 26a
Um disco uniforme de e raio está sobre uma superfície de gelo lisa. Duas patinadoras gêmeas enrolam cordas em torno do disco, num mesmo sentido. Depois cada qual puxa a sua corda e se afasta do disco, exercendo sobre ele forças constantes e durante .
Determine a aceleração, a velocidade e a posição do centro de massa em função do tempo.
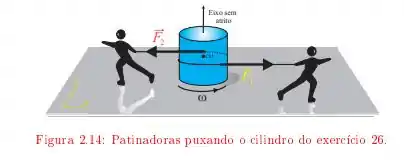
Passo 1
Oiie, tudo bem?
Temos aqui um disco uniforme que é puxado por duas patinadoras como no esquema a seguir
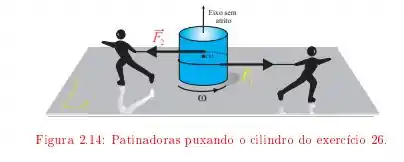
este disco tem uma massa e raio . Elas aplicam forças e de forma que o giro do disco é acelerado por ambas as forças durante , o objetivo desta alternativa é
Determine a aceleração, a velocidade e a posição do centro de massa em função do tempo.
O segredo aqui é utilizar o módulo da força para encontrar a aceleração linear. Temos que cada patinadora puxa em um sentido, mesmo que estejam puxando em posições diferentes do cilindro, vamos considerar para esta alternativa que a intensidade da força sentida no centro de massa é a mesma que nas extremidades e usar a segunda lei de Newton! Saca só!
Passo 2
Usando a segunda lei de Newton como
as duas forças estão em sentidos opostos, portanto, temos que
portanto, a aceleração do centro de massa é dada por
Essa é uma aceleração constante, portanto, consegue se lembrar como obter a velocidade e posição? Vem comigo!
Passo 3
A velocidade pode ser obtida pela relação
e, pela equação horária do movimento retilíneo, temos que
Ótimo! A primeira alternativa já foi! Te vejo na próxima!
Resposta
, e