Dois blocos estão em contato em uma mesa sem atrito. Uma força horizontal é aplicada ao bloco maior, como mostra a Figura. Se e .
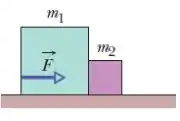
Mostre que se uma força de mesmo módulo de for aplicada ao menor dos blocos no sentido oposto, o módulo da força entre os blocos será , que não é o mesmo valor calculado no item anterior.
Passo 1
Faaaala gente bonita, tudo beleza?
Nessa questão temos dois blocos que estão coladinhos, e se movem pela aplicação de uma força . No item anterior, usando a segunda lei de Newton, vimos que a força de contato entre os blocos valia:
Aí nesse item o enunciado propõe mudarmos um pouco a brincadeira, ao invés da força ser aplicada no bloco , vamos aplicá-lo no bloco . Qual será a nova força de contato entre os blocos?

Vamos usar a mesma ideia do item anterior, e escrever a segunda lei de Newton para os blocos:
Onde:
é a força resultante;
é a massa do objeto;
é a aceleração do objeto;
Vamo nessa!
Passo 2
No bloco , na horizontal, atuam apenas a força e a normal de contato entre e (em sentido oposto á ).
Daí:
Já no bloco , na horizontal, atua apenas a força de contato entre entre os blocos, sendo ela a responsável por movimentar . Além disso, como e estão colados, eles precisam ter a mesma aceleração.
Daí:
Substituindo esse resultado na primeira equação, vem:
Logo:
Portanto:
Passo 3
Agora que já encontramos a aceleração, pra calcular a força de contato basta substituir o resultado
na equação da força resultante do segundo bloco:
Logo:
Olha aí pessoal, quando mudamos o ponto de aplicação da força, a força de contato também muda. Mas, a aceleração permanece a mesma 😊
Valeu gente, até mais!