[Enunciado comum às Questões 5 e 6]
Sobre um corpo, de massa , atuam três forças, , e . Duas delas, mostradas na figura abaixo à esquerda, tem módulos iguais a , mas atuam em direções diferentes. O corpo está inicialmente em repouso sobre uma mesa horizontal sem atrito. Na figura da direita, é mostrado um gráfico da velocidade escalar do corpo em função do tempo, onde cada quadrado na vertical equivale a . Considere e .
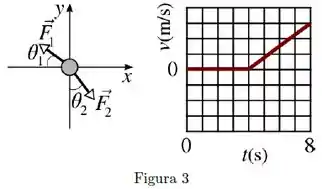
[Questão 5]
Considere as assertivas para o instante :
.
.
.
Marque a alternativa abaixo contendo apenas as assertivas corretas.
(a)
(b)
(c)
(d) e
(e) e
(f) e
(g) Todas
(h) Nenhuma
Passo 1
Queremos saber sobre o instante .
Dá uma olhada naquele gráfico da velocidade o instante :
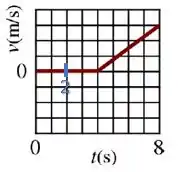
A velocidade é zero e não está variando.
Isso indica que o corpo não sofre aceleração e portanto está em equilíbrio de forças:
Beleza, vamos olhar as afirmativas.
Passo 2
Vamos começar com a , porque ela é bem direta a partir da ideia que acabamos de ver.
.
Vimos que o corpo está em equilíbrio, já que não está sofrendo nenhuma aceleração.
Então, o somatório de forças tem que ser zero:
Ou seja:
Quando somamos vetores, as suas direções estão sendo levadas em consideração.
Por exemplo, se tivéssemos essa situação:
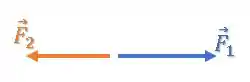
Se esse sistema está em equilíbrio, isso significa que a soma vetorial é nula e escrevemos isso somando os vetores, por mais que eles estejam em sentidos opostos:
Agora, se estivermos calculando a partir dos módulos, temos que:
Ou simplesmente:
Sacou?
Então, a afirmativa está correta.
Passo 3
.
Poderíamos decompor todas aquelas forças e descobrir a direção e o módulo de para depois comparar com esse valor.
Porém, essa afirmativa só estará correta em um caso específico, onde tanto a força quanto a força apontam na mesma direção e sentido e a força equilibra as duas apontando para o sentido oposto:
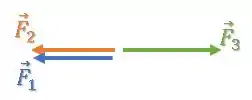
Como a situação da questão é diferente disso, a afirmativa é falsa.
Passo 4
.
Aqui faremos a mesma coisa, essa relação aí só acontece para um caso específico.
Repara que isso parece bastante com um Pitágoras, né?
Isso mesmo!
Se os vetores e estiverem perpendiculares entre si, o vetor resultante entre eles será:
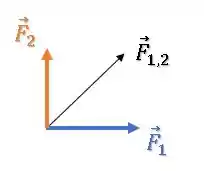
E seu módulo:
Para equilibrar esse sistema aí, a força deve ter o mesmo módulo de e apontar no sentido oposto:
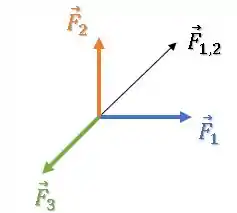
Como a situação que temos é diferente, a afirmativa também está incorreta.
Resolvendo assim, com menos contas, temos que apenas a está correta, então ficamos com a letra (c).
Resposta
Letra (c)