Questão 3
Considerando um cubo de 8m³ com 7m³ de água apoiado sobre um caminhão em movimento, qual aceleração máxima que o caminhão pode ter para que esse líquido não transborde?
Passo 1
Fala galerinha tranquilidade, essa é uma questão muito interessante, o que vamos precisar para essa parte é uma avaliação vetorial, vamos desenhar para entender o que está acontecendo.
Aresta do Cubo (preto)
Aresta da água(azul)
Sendo esses valores para o sistema estacionário.
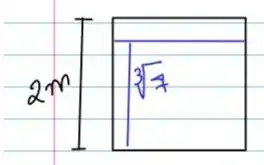
Passo 2
Agora precisamos avaliar o que vai acontecer quando o caminhão entra em movimento, vamos considerar que a altura máxima que a água pode chegar na caixa é a aresta da caixa cúbica, então a configuração será a seguinte:
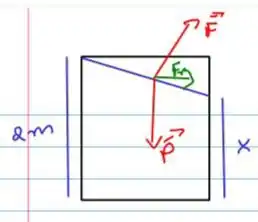
Nesse caso temos a força peso que é do líquido, a força F que equilibra o líquido com essa configuração dentro da caixa, e a resultante entre elas que é a força verde.
Agora podemos fazer a análise vetorial e verificar quais as componentes que serão necessárias.
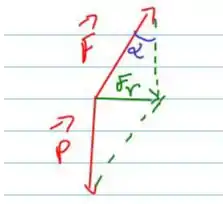
Passo 3
Agora encontramos a relação entre a aceleração e a gravidade no entanto não sabemos o ângulo alfa, porém temos o pequeno triangulo da parte de cima da caixa, se nós conhecermos as dimensões dele podemos encontrar o valor da tangente.
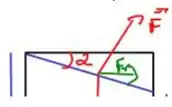
Sabemos a parte da base do triângulo, que vale 2 m, fica faltando a altura, que seria o quanto aumentos antes de o caminhão entrar em movimento.
Ficando:
Esse resultado podemos subtrair do valor da aresta da água, ficando:
Agora encontramos a tangente que nos faltava, ficando :
Resposta
Sendo o resultado a alternativa C