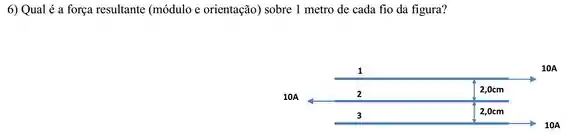
Passo 1
A força por unidade de comprimento (sobre metro) entre dois fios é igual a:
Na teoria vimos que essa equação é determinada por meio de uma combinação entre a lei de Ampère a a fórmula do BILL. Lembre-se:
- Fios com correntes no mesmo sentido se atraem
- Fios com correntes de sentidos opostos se repelem
Assim, aqui não é válida a frase “os opostos se atraem e os iguais se repelem”, isso vale só pra lei de Coulomb ok?
Passo 2
Por simetria, a resultante das forças no fio é igual a zero. Isso porque os fios e puxam o fio do meio com a mesma força mas para lados diferentes. Logo: . (Já garantimos uns décimos aqui sem fazer muitas contas).
Passo 3
No fio :
- O fio exerce uma força de repulsão por unidade de comprimento igual a:
- O fio exerce uma força de atração por unidade de comprimento igual a
Prevalece a força de repulsão, subtraindo ela da atração temos:
E essa força está direcionada para cima, em direção ao fio . Algo análogo acontece com o fio : por simetria, esse fio é puxado para baixo com uma força de mesmo módulo por unidade de comprimento, igual a .