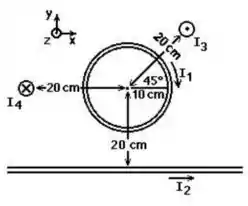
2ª questão - Uma espira circular de raio e três longos fios retos conduzem correntes de , , e , respectivamente, como mostrado. Cada fio reto está a do centro da espira. Na Figura abaixo, a componente do campo magnético resultante no centro da espira será:
A)
B)
C)
D)
E)
Passo 1
Fala aí!! Bem-vindo! Está tendo um pouco de dificuldades nessa questão? Não se preocupe vou fazer o máximo pra te ajudar. 😉👍

Para essa questão, temos um ponto qualquer no espaço que está centrado em um fio circular de raio que é percorrido por uma corrente e também temos outros três fios que são dispostos a uma distância de do ponto que conduzem as correntes , e assim como vemos na imagem do enunciado.
Nosso objetivo com essas informações é obter a componente do campo magnético no ponto que estamos estudando.
E então, como fazemos isso? 🤔🤔
O campo magnético produzido por um fio condutor segue a regra da mão direita, lembra?
Colocando nossa mão direita em um fio condutor com o polegar voltado para a direção do fluxo de correte conseguimos exemplificar o campo magnético pelo movimento dos nossos dedos ao abraçar o fio.
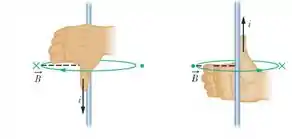
Vamos usar esse método pra nos ajudar a obter o campo magnético!
Bora lá? 😁
Passo 2
Vamos analisar fio a fio e no fim somar as contribuições de cada um na direção do campo total.
Vale lembrar que pela imagem do enunciado, o semieixo positivo de aponta para cima, o semieixo positivo de aponta para a direita e o semieixo positivo de aponta para fora da tela (em nossa direção).
Primeiro vamos analisar o fio circular que é percorrido pela corrente .
Se colocarmos a mão direita com o polegar apontando para a direção da corrente, vemos que o movimento dos nossos dedos aponta para dentro da tela no ponto.
Ou seja, o campo magnético gerado pelo fio aponta para o semieixo negativo de então não contribui para nosso problema, logo, podemos descarta-lo.

Entendeu? Vamos ver outro fio! 😉
Passo 3
Agora vamos analisar a contribuição do fio que é percorrido pela corrente !
Fazendo a regra da mão direita, vemos que com nosso polegar apontando no sentido da corrente, o movimento dos nossos dedos ao abraçar o fio nos diz que o campo magnético aponta para fora da tela no ponto, ou seja, aponta para positivo, logo, também não há contribuição para o nosso problema.
Vamos ver o próximo!

Está acompanhando? 😎
Passo 4
Analisando o fio que flui a corrente pela regra da mão direita, vemos que, no ponto, o campo magnético aponta para baixo com uma inclinação de para a direita, ou seja
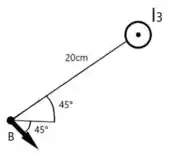
O módulo do campo magnético no caso de um fio infinito, como no caso, é dado por
Onde é uma constante que vale , é a corrente que no enunciado nos diz que vale e é a distância do fio ao ponto que vale .
Substituindo essas informações em , temos
Vamos guardar essa informação para mais tarde!
Bora ver o último fio!
Passo 5
Para o fio que é percorrido pela corrente , fazendo a regra da mão direita vemos que como a corrente é indicada entrando na tela (negativo de ), o movimento dos nossos dedos aponta para baixo no ponto, ou seja, o campo magnético é dado por
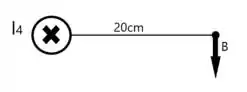
Logo, vemos que o módulo do campo magnético aponta para negativo.
A fórmula para obter o módulo do campo é o mesmo para esse caso, já que estamos lidando com outro fio infinito.
A única diferença é que nesse caso a corrente é na verdade que no enunciado é dada como e a distância permanece a mesma de .
Tranquilo até aqui? 👀
Passo 6
Agora vem o passo final para resolver esse problema! Acabamos de obter os módulos dos campos magnéticos que nos interessam para resolver esse problema, no caso, e .
Esses campos estão dispostos na seguinte forma.
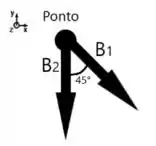
Temos dois vetores e queremos saber a resultante com relação ao eixo , como fazemos? 🤔
Já vemos de cara que aponta para então não precisamos fazer muitas coisas.
Mas para obter a resultante de em , temos que aplicar o seno do ângulo que o vetor faz com o eixo, não é? Ou seja
O sinal negativo nos diz que a resultante aponta para baixo, para o sentido negativo de .
Substituindo e , temos
Assim o campo magnético resulta em
Analisando as alternativas do problema, vamos que a alternativa que condiz com nosso resultado é a letra A)! .
É isso! Essa resolução te ajudou? Responde Aí! ✌

Resposta
A)