UFRJ – Física 3 – 2020.2 – PF – M.Escolha
Seja um segmento reto de fio de comprimento , por onde passa uma corrente estacionária de intensidade (suprida por um circuito conectado a este segmento).
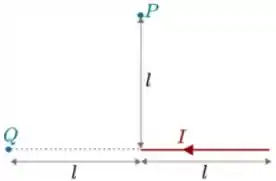
Considere os pontos e dados na figura. A intensidade do campo magnético produzido pelo segmento nestes pontos vale:
Escolha uma:
. e
. e
. e
. e
e. e
Passo 1
Vem comigo que a gente resolve essa juntos!
Para achar o campo em e em vamos usar a expressão que fornece o campo para um fio finito, ela é dada por:
Onde e são os seguintes ângulos:
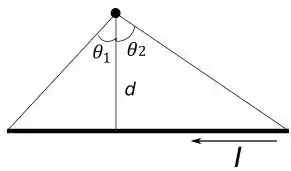
Então com isso podemos calcular o campo nos pontos que queremos.
Passo 2
Vamos começar com o ponto , temos que e são zero, assim:
Passo 3
Agora vamos para o ponto .
Nesse ponto temos , para vamos usar a trigonometria ao nosso favor para encontrarmos .
Sabemos que o seno de um ângulo é o cateto oposto sobre a hipotenusa, a hipotenusa do triangulo formado pelo fio e o ponto é dada por:
Então temos que:
Então temos o seguinte para o campo magnético:
Resumindo, temos que:
Então a nossa alternativa vai ser a letra .
Resposta
. e