14 - Uma espira condutora no formato de uma elipse conduz uma corrente . Suficientemente próximo de qualquer ponto da espira, podemos afirmar que:
- Quando estamos muito próximos do fio, podemos aproximar o campo magnético pelo campo no centro de uma espira circular, pois a elipse se aproxima por um círculo.
- O campo magnético é nulo devido ao fato de a lei de Biot-Savart nos dizer que o campo magnético diminui quanto próximo de sua fonte.
- Quando estamos muito próximos do fio, podemos aproximar o campo magnético pelo campo do fio infinito uma vez que a curvatura do fio se torna imperceptível.
- O campo magnético é radial ao fio, como em todo condutor em equilíbrio estático.
- Não há como fazer esse cálculo, pois não há simetria suficiente.
Passo 1
Ora, a resposta correta aqui é a letra . Mas por quê?
Bem, se você de fato começa a dar um zoom nessa elipse ela se torna, bem próximo dela, podemos ver que a curvatura “desaparece” de tão imperceptível que ela se torna!
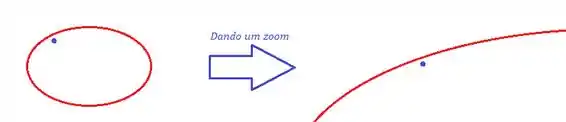
Então de fato, bem próximo dela, podemos considerar um fio reto e gigante (infinito), saca?
Passo 2
Mas para você que está curioso em saber qual é o erro das outras alternativas aqui vãos nós:
- A letra A se fala que podemos aproximar o campo no centro, o que não é verdade, pois sabemos que o campo magnético depende da distância do fio ao ponto de medição. Um ponto próximo do fio tem distância diferente do ponto no centro.
- A letra B fala que o campo é nulo, o que já está errado, e para piorar ela fala que o campo diminui à medida que nos aproximamos da fonte (o fio com a corrente ). O que não é verdade, o campo aumenta.
- A letra D até acerta ao falar que o campo é radial, mas erra ao dizer que ele é gerado em um condutor em equilíbrio estático. Deveria ser equilíbrio dinâmico afinal a corrente de elétrons não é estática (parada) e sim em um movimento constante (equilíbrio dinâmico).
- Letra E: dá para fazer o cálculo, basta aproximar por um fio como vimos na resposta correta!
Resposta
Letra C.