Três fios paralelos e muito longos conduzem correntes de módulo igual a , com os sentidos indicados na Figura abaixo. Sabendo que a distância entre dois fios adjacentes é igual a , calcule o módulo, a direção e o sentido da força magnética resultante por unidade de comprimento sobre cada fio.
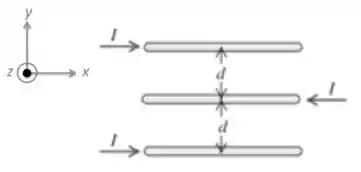
Passo 1
Para gente calcular a força resultante em cada um dos fios acima, precisamos saber qual é o campo magnético resultante sobre cada um deles devido a todos os outros.
No primeiro fio de cima, o módulo vetor campo magnético resultante será
Esse campo magnético está entrando no plano da página, de modo que o vetor é
A força que age nesse fio é
Portanto, a força por unidade de comprimento é dada por
Passo 2
Já no fio do meio, o campo resultante será nulo, pois as correntes dos fios de cima e de baixo produzem um campo que tem mesmo módulo, mesma direção, mas sentidos contrários e, por isso, se cancelam.
Portanto, a força por unidade de comprimento que age no fio do meio é NULA.
Passo 3
Por último, o módulo vetor campo magnético resultante no último fio de baixo será
Esse campo magnético está saindo do plano da página, de modo que o vetor é
A força que age nesse fio é
Assim, temos que a força por unidade de comprimento no último fio de baixo é dada por
Resposta
Primeiro fio de cima:
Fio do meio:
Fio de baixo: