Três fios condutores retilíneos paralelos e com comprimento infinito se encontram no mesmo plano , com o fio condutor central que coincide com o eixo , como mostrado nas figuras abaixo. A distância entre os fios condutores contíguos é . O condutor central é percorrido por uma corrente constante no sentido , enquanto os dois condutores laterais são percorridos cada um por uma corrente no sentido oposto .
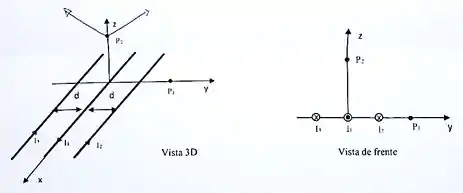
Determine (deixe os cálculos em função de ):
(a) O campo magnético gerado pelos três condutores no ponto com coordenadas .
(b) O campo magnético gerado pelos três condutores no ponto com coordenadas .
(c) A força por unidade de comprimento experimentada pelo condutor central devida ao campo magnético produzido pelos outros dois condutores.
(Sugestão: lembre-se que, por Ampère, o módulo do campo magnético produzido por um fio infinito em uma distância é dado por: ).
Passo 1
Para o item (a), somamos a contribuição no campo magnético de cada fio em . Pela regra da mão direita, sabemos que os fios 2 e 3 geram um campo magnético apontando para baixo, enquanto que o fio 1 gera um campo magnético que aponta para cima.
Temos:
Passo 2
Já no ponto , pela regra da mão direita, sabemos que o fio 1 produz um campo apontando para a esquerda, no sentido negativo de . Já os fios 2 e 3 produzem campos e mostrados na figura abaixo (as direções dos campos e são tangenciais às circunferências).
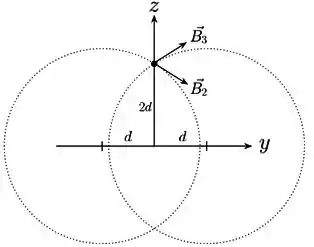
Temos:
Passo 3
Vamos calcular o módulo de cada uma das forças (por unidade de comprimento):
Como as correntes entre os fios 2 e 1 e entre os fios 3 e 1 são antiparalelas, eles vão se repelir! Ou seja,
.
A força resultante será, portanto:
Resposta
(a) (direção do eixo , sentido positivo), (direção do eixo , sentido negativo), e (direção do eixo , sentido negativo).
(b) (direção do eixo , sentido negativo), (direção e sentido mostrados na figura) e (direção e sentido mostrados na figura).
(c)