Dois fios retilíneos muito longos, paralelos, transportam correntes de mesma intensidade e sentido, conforme a figura abaixo.
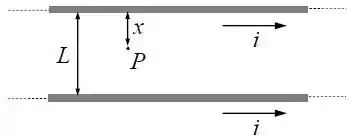
A distância entre os fios é e o ponto encontra-se a uma distância de um dos fios. A intensidade do campo magnético no ponto , e da força magnética por unidade de comprimento, , que um fio exerce sobre o outro são:
Passo 1
O campo magnético gerado por um fio retilíneo é dado por:
Utilizando a regra da mão direita, vemos que os campos magnéticos gerados pelos dois fios possuem sentidos distintos. Logo, o campo magnético resultante no ponto será:
Onde um dos fios está a uma distância do ponto , enquanto o outro está a uma distância , logo:
Colocando em evidência os termos em comum, teremos:
Passo 2
A força magnética sobre um fio retilíneo é dada por:
Onde é o campo magnético que atua sobre o fio, é o seu comprimento e é o ângulo entre o campo magnético e o sentido da corrente no fio.
Assim, a força magnética entre dois fios é dada por:
No nosso caso, queremos saber a força por unidade de comprimento entre dois fios separados por uma distância , logo:
As duas correntes possuem o mesmo valor, logo:
A resposta certa é a letra .
Resposta