Na figura abaixo, quatro fios retilíneos longos são perpendiculares ao papel, e suas seções retas formam um quadrado de lado .
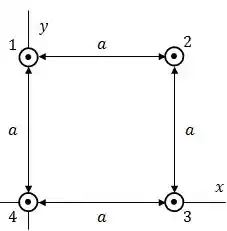
Todos os fios conduzem correntes de para fora do papel. Em termos dos vetores unitários, qual é a força magnética por metro de fio que age sobre o fio 1?
Passo 1
Ok, vamos começar definindo os as forças que agem sobre o fio 1.
Como todas as correntes são iguais, os módulos de cada força serão:
Passo 2
Beleza, agora que já definimos os módulos, precisamos olhar para os vetores. Como todos os fios possuem correntes paralelas, todas as forças serão atrativas, logo:
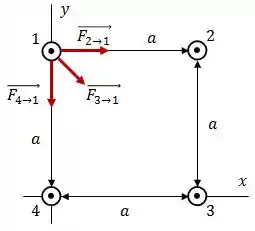
Assim, as forças serão dadas por:
Passo 3
Assim, a força resultante sobre o fio 1 será:
Por fim, a força resultante por unidade de comprimento será:
Onde:
Finalmente:
Resposta
Exercícios de Livros Relacionados
Dois fios estão no plano da página e conduzem correntes em sentidos opostos, como mostrado na figura 27-48. Em um ponto na metade da distância entre os fios, o campo magnético é ( a ) zero b para dent
Determine a magnitude da força por unidade de comprimento exercida por um fio sobre o outro.
Dois fios longos, retilíneos e paralelos, separados por 8,6c m , conduzem corrente iguais. Os fios se repelem com uma força de 3,6 n N / m por unidade de comprimento. (a) As correntes são paralelas ou
Como um estudante técnico, você está preparando uma aula de demonstração sobre “suspensão magnética”. Você tem um fio rígido, retilíneo, de 16c m de comprimento, que será suspenso por guias flexíveis,
Três fios longos, retilíneos e paralelos passam pelos vértices de um triângulo equilátero que tem lados iguais a 10 cm, como mostrado na Figura 27-53. Um ponto indica que o sentido da corrente é para