UFF - Física 2 – P2 2018.1 - 5
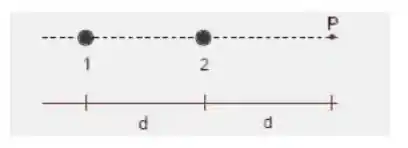
A figura abaixo representa dois fio bastante longos (1 e 2) perpendiculares ao plano do papel, percorridos por correntes de sentido contrário, e , respectivamente. A condição para que o campo magnético resultante, no ponto , seja zero é:
Passo 1
Aqui, precisamos nos lembrar que o módulo do campo magnético produzido por uma corrente passando em um fio longo (“infinito”) em um ponto a uma distância é:
e esse campo é sempre perpendicular ao ponto .
No caso do nosso problema, os campos e produzidos pelas correntes e são perpendiculares ao ponto , estão na mesma direção, mas têm sentidos contrários, já que as correntes estão passando em sentidos contrários nos fios longos 1 e 2.
Para que o campo resultante em seja nulo, e precisam ter sentidos contrários, mas também precisam ter mesmo módulo. Por isso, igualando os módulos desses campos, vamos ter que:
Resposta
Letra b.