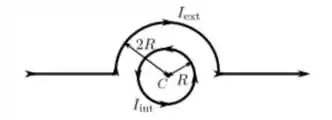
10) Um fio fino circular, de raio , é percorrido por uma corrente estacionária de intensidade . No mesmo plano, temos um outro fio, constituído por dois segmentos retilíneos longos e um arco de semicircunferência, concêntrico com o primeiro fio, de raio , conforme mostra a figura. Qual deve ser a intensidade da corrente estacionária , nesse segundo fio, para que o campo magnético no centro comum seja nulo?
a)
b)
c)
d)
e)
Passo 1
Iae, meus queridos! Está com dificuldades nessa questão? Não se preocupe! Estamos aqui para ajudar 😉

Nesse problema temos dois fios onde o primeiro é um fio circular de raio que flui uma corrente no sentido anti-horário. O segundo fio faz um arco de e raio concêntrico com o primeiro fio que flui uma corrente no sentido horário.
Podemos ver o que acabamos de descrever como
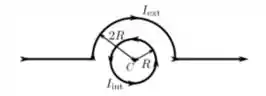
O que queremos saber é qual deve ser a corrente com relação a para que o ponto tenha um campo magnético nulo.
Tem ideia do que fazer nessa questão?? 🤔🤔
O campo magnético produzido por uma corrente segue a regra da mão direita, não é?
Colocando a palma da mão sobre o fio com o dedão apontando no sentido da corrente, o movimento dos nossos dedos ao abraçar o fio é o mesmo sentido do campo magnético.
Lembra disso? 😁
Passo 2
Assim, fazendo a regra da mão direita para o primeiro fio de raio , vemos que o sentido do campo magnético no ponto é dado para fora da tela.
Já para o arco de raio , fazendo a regra da mão direita vemos que o sentido do campo magnético aponta para dentro da tela no ponto .
Essa informação é muito importante pois vemos que os campos apontam em sentidos opostos no ponto .
Portanto para o campo ser nulo no ponto, os seus valores absolutos devem ser iguais.
Mas como calculamos esses campos? 🤔
Para arcos e círculos, o campo magnético é dado por
Onde é a corrente do fio, é o ângulo em radianos que o fio faz no ponto e é a distância até o ponto, ou seja, o raio.
Vamos chamar o campo produzido pelo primeiro fio de e o campo produzido pelo segundo fio.
Perceba que as partes que estão retas no segundo fio não influenciam no resultado pois se prolongarmos as retas, vemos que elas passam justamente no ponto .
Entendeu? Bora começar! 😉
Passo 3
Começando pelo fio , temos que a corrente que flui por ele é , o ângulo em radianos que ele faz no ponto é uma volta completa, ou seja, e o raio é .
Portanto é dado por
Simplificando a fração cortando e fazendo , temos
Agora para o fio , a corrente que flui por ele é , o ângulo em radianos que ele faz com o ponto é meia volta, ou seja, e o raio é .
Logo, é dado como
Simplificando cortando e fazendo , vamos obter
Como o módulo dos campos devem ter o mesmo valor e e representam os módulos dos campos de cada fio, vamos igualar e .
Podemos simplificar a igualdade cortando e dos dois lados
Isolando em um lado passando multiplicando , temos
Com isso vemos que a corrente deve ser vezes maior que a corrente para que o campo magnético no ponto seja nulo!
Assim vemos que a letra a) é a alternativa que condiz com nosso resultado.
É isso, espero ter ajudado! Entendeu tudo? Responde Aí! 😎👍

Resposta
a)