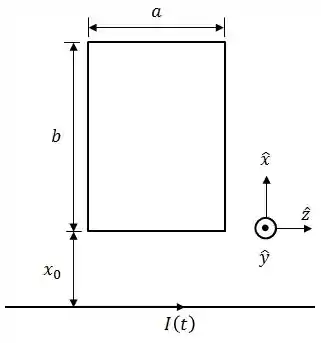
Uma espira retangular no plano , de autoindutância desprezível, tem lados e e resistência . Um fio retilíneo infinito, por onde flui uma corrente dependente do tempo , é colocado ao longo do eixo a uma distância da espira, conforme mostra a figura. Despreze as correntes de deslocamento do sistema.
Sabendo que o campo produzido pelo fio retilíneo em um ponto é dado por , onde é a distância de ao fio e é o vetor unitário que “circula” em torno do fio, encontre .
Calcule o fluxo magnético através da espira, tomando como o unitário normal à superfície.
Supondo que , determine a força eletromotriz induzida na espira?
Passo 1
Sabendo que o campo produzido pelo fio retilíneo em um ponto é dado por , onde é a distância de ao fio e é o vetor unitário que “circula” em torno do fio, encontre .
Vamos considerar primeiro, só um pedaço do fio de comprimento L. O campo que esse pedaço de fio produz num ponto P é dado pela lei de Biot-Savart por:
Como o fio é infinito, isso significa que , então:
Passo 2
Calcule o fluxo magnético através da espira, tomando como o unitário normal à superfície.
Por definição, o fluxo magnético é dado por:
Vamos analisar graficamente esse cara:
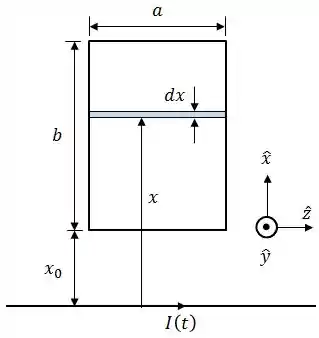
Daqui podemos tirar que:
Nessa região, o campo magnético é dado por:
Portanto:
Finalmente:
Passo 3
Supondo que , determine a força eletromotriz induzida na espira?
De acordo com a lei de Faraday, a induzida na espira é dada por:
Onde:
Portanto:
Resposta