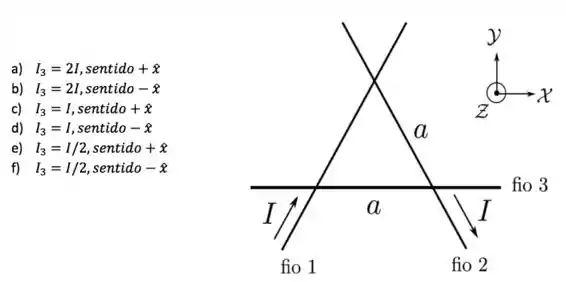
Três fios condutores finos, retilíneos e infinitos são dispostos sobre o plano de um sistema de coordenadas, de forma que um deles é paralelo ao eixo e a região definida pela interseção dos três fios é um triângulo equilátero de lado , como mostrado na figura abaixo. Dois destes fios carregam correntes estacionárias de mesma intensidade e sentidos indicados na figura. Quais devem ser a intensidade e o sentido da corrente estacionária no terceiro fio para que o campo magnético no centro do triângulo seja nulo?

Como temos fios infinitos percorridos por uma corrente estacionária, então o módulo campo magnético gerado depende apenas da corrente e da distância , perpendicular ao fio, onde se deseja calcular o campo

O sentido e a direção desse campo é dado pela regra da mão direita.

No caso desta questão, queremos analisar o campo magnético no ponto , que é o centro da figura abaixo. Portanto, este ponto está à mesma distância dos vértices do triângulo equilátero.

Por essa razão, este ponto está também à mesma distância dos três fios indicados na figura.

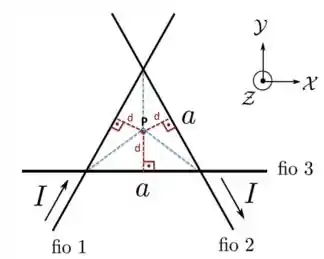
Antes de seguir para o cálculo do campo, a gente vê que o campo produzido pelas correntes mostradas na figura está entrando na página, isto é, está na direção e sentido de .

Para que o campo produzido por uma corrente no fio 3 possa cancelar o campo produzido pelos fios 1 e 2, essa corrente deve produzir um campo na direção e no sentido de . Portanto, no fio 3 deve haver uma corrente no sentido .

Resta ver como é a corrente neste fio 3...