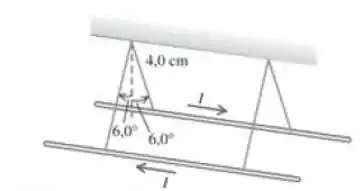
Dois fios longos e paralelos estão suspensos por meio de cordas de de comprimento, presas a um eixo comum, como mostra a Figura abaixo. Os fios possuem massa por unidade de comprimento igual a e conduzem correntes de mesmo módulo, porém de sentidos contrários. Qual é a corrente em cada fio, sabendo que as cordas de sustentação formam um ângulo de com a vertical?
Passo 1
Para matar esse exercício, imagina que você está vendo a Figura acima de perfil, como na Figura abaixo, de maneira que a corrente no fio da esquerda está entrando no plano da página e a da direita saindo da página.
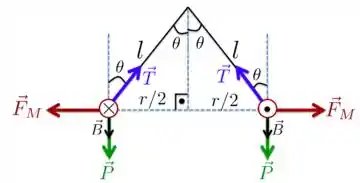
A corrente da esquerda produz um campo magnético no fio da direita que aponta para baixo. Isso você pode verificar usando a regra da mão direita para corrente. Um campo de mesma intensidade é produzido pela corrente da direita no fio da esquerda e aponta também para baixo. Esses campos têm uma intensidade que é dada por
Como é perpendicular às correntes em ambos os fios, então a força magnética que age nos dois fios tem mesma direção, mesma intensidade, porém sentidos diferentes, como está mostrado na Figura. Por isso, os fios nessa situação de afastam um do outro. A intensidade dessa força é
em que é o comprimento dos fios percorridos pelas correntes e é a distância entre os dois fios.
Passo 2
Como os fios estão em equilíbrio com as cordas de comprimento fazendo um ângulo com a vertical, vamos escrever as componentes das forças em cada um dos eixos. Fazendo isso, vamos encontrar
Se a gente divide a primeira equação acima pela segunda, obtemos o seguinte
Colocando aqui dentro a expressão que encontramos lá no Passo 1, temos
Bom, nessa fórmula, ainda não conhecemos o valor de nem de (não confunda esse comprimento com , que o comprimento das cordas que estão segurando os fios!!), que são quantidades não fornecidas pelo enunciado. Vamos continuar...
Passo 3
Para completar, vamos deixar a expressão para a corrente acima em termos apenas das quantidades fornecidas pelo enunciado.
Para isso, o exercício diz que a massa dos fios percorridos pela corrente pode ser escrita como
em que é conhecido, mas não sabemos o valor de , mas isso não vai ser um problema, como você vai ver logo logo! :-).
Continuando, da Figura acima, a gente tem também que
e aqui , comprimento das cordas, é conhecido. Colocando isso tudo junto lá na expressão para , chegamos no seguinte
que não depende do comprimento dos fios percorridos pela corrente . Tranquilo?
Colocando os valores dados no enunciado dentro dessa expressão, com a ajuda da nossa amiga calculadora, você vai encontrar que o valor da corrente é