Dois fios retilíneos muito longos transportam correntes paralelas ao longo da direção um deles transporta a corrente no sentido , e o outro transporta uma corrente . Na figura mostram-se o ponto , de coordenadas , e o campo magnético em devido somente ao fio .
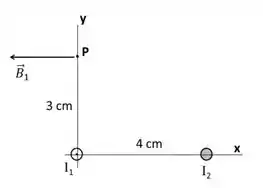
A fim de que o campo resultante no ponto (devido a ambos os fios) possua direção , qual deve ser o sentido e quanto deve valer a corrente ?
Suponha que o campo resultante seja dado por: . Um terceiro fio retilíneo e muito longo transportando corrente no sentido é colocado passando por . Encontre, na unidade , o vetor força por unidade de comprimento que o terceiro fio sofre.
Passo 1
Para resolver esse item, devemos pensar na amperiana que tem o fio no centro e passa pelo ponto . Se a corrente estiver saindo, temos que o campo em aponta para baixo(vetor laranja), e se estiver entrando, o campo em aponta para cima(vetor verde), se liga!
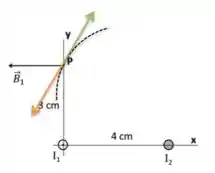
Para que o campo se anule na direção e sobre apenas componente , temos que a única opção possível é que o campo aponte na direção do vetor verde, ou seja, a corrente deve estar entrando! Agora vamos determinar seu valor. Para que não tenhamos componente a componente do vetor campo gerado pelo fio deve cancelar .
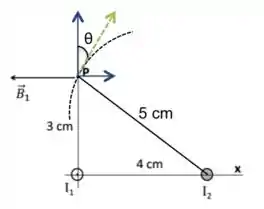
Repare que temos que a distância do ponto até o fio é pois temos um triângulo , além disso, temos que !
Substituindo o valor do campo para um fio infinito temos:
Passo 2
Agora temos um novo problema, temos um fio no ponto que transporta corrente no sentido , o campo magnético no ponto é . A força sofrida por esse fio será dada pela seguinte relação:
Nesse caso, temos que e foi dado, substituindo, temos:
Como queremos a força por unidade de área, devemos passar para o outro lado dividindo!
Resposta
no sentido