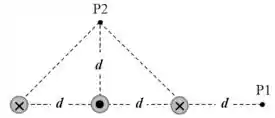
Três fios retilíneos e longos, separados a uma distância igual a , são percorrido por uma corrente elétrica igual a . Eles são paralelos e dispostos conforme a figura abaixo. Calcule e indique na figura o vetor campo magnético nos dois pontos, e .
Passo 1
Vamos primeiro determinar o campo em , para isso, vamos utilizar a Linda Lei de Ampère, ela nós fiz:
Para o fio mais à esquerda, iremos chamá-lo de fio . Traçaremos uma amperiana cujo centro está no fio e o raio vale , nesse caso, como é sempre paralelo a , temos:
Pela regra da mão direita, temos, em que ele aponta para baixo, adotaremos a convenção de que para baixo é negativo, então:
Para o fio ao lado, fio , temos:
Pela regra da mão direita, temos que o campo em aponta para cima, usando a nossa convenção, temos:
Para o último fio, fio , temos:
Pela regra da mão direita, temos que o campo em aponta para baixo, usando a nossa convenção, temos:
Para determinar o campo em , basta somar os campos que achamos!
Portanto o campo em aponta para baixo!
Passo 2
Vamos usar o mesmo processo para calcular o campo em , mas temos que ficar atentos com a direção dos campos. Vou começar calculando o campo gerado pelo fio , que é o mais fácil de visualizar:
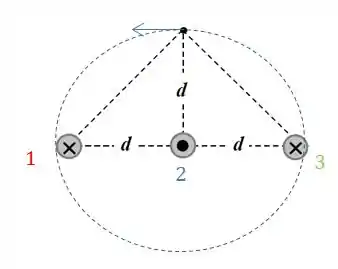
O campo gerado por ele, pela regra da mão direita, aponta para a esquerda no ponto e seu valor será:
E se considerarmos que para a direita é positivo, podemos escrever:
(negativo pois aponta para a esquerda e o vetor unitário aponta pra direita.)
Agora, vamos ver o campo formado pelo fio e pelo fio :
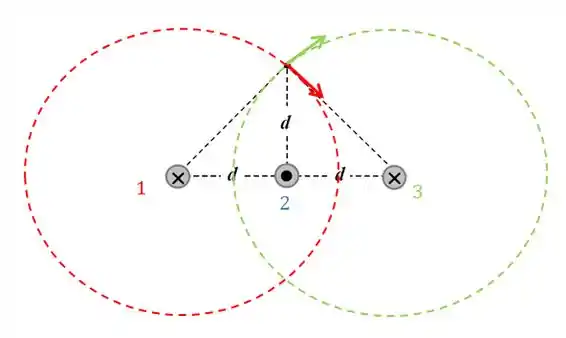
Esses campos irão possuir tanto componente em quanto em .
Os dois campos vão ter o mesmo valor em módulo (por conta da simetria do problema).
E para encontrar esse módulo, faremos:
Nese caso, precisamos determinar
Substituindo para achar o campo:
Agora para encontrar suas componentes, precisamos olhar mais a fundo esses vetores:
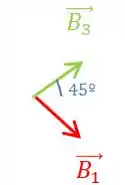
Brincando um pouco de trigonometria, você vai encontrar que o ângulo que o vetor campo faz com a horizontal é (é o mesmo ângulo que o triângulo isósceles da figura).
A componente vertical desses campos, por eles serem simétricos irão se anular, por isso não precisamos nem calcular.
A componente horizontal vai ser dada como:
E a componente horizontal do campo dado pelo fio , dá o mesmo valor (o que faz sentido né).
Encontramos portanto, o campo dado pelo fio que aponta para a esquerda e que o campo formado pelo fio e irão se anular na vertical e irão se somar para a direita.
Sendo assim, podemos encontrar o campo no ponto .
Considerando para direita como positivo:
Portanto o campo em será nulo. As componentes horizontais dos campos gerados pelos fios 1 e 3 irão anular o campo gerado pelo fio 2.
Resposta