A figura abaixo mostra, em seção reta, quatro fios finos paralelos, retilíneos e muito compridos, que conduzem corrente iguais nos sentidos indicados.
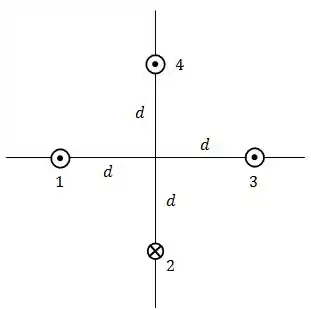
Inicialmente, os quatro fios estão a uma distância da origem do sistema de coordenadas onde criam um campo magnético total .
Para que valor de o fio 1 deve ser deslocado sobre o eixo para que o campo sofra uma rotação de no sentido anti-horário?
Com o fio 1 na nova posição, para que valor de o fio 3 deve ser deslocado sobre o eixo para que o campo volta à orientação inicial?
Passo 1
O primeiro passo é ver onde está o campo magnético original. Como as correntes são iguais e as distâncias iniciais também são, os módulos dos campos magnéticos de cada fio também serão iguais.
Logo, usando a regra da mão direita, podemos determinar para onde estão esses campos:
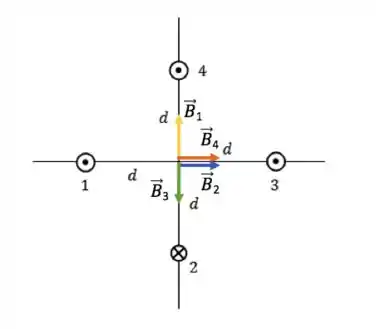
Assim, o campo magnético resultante será:
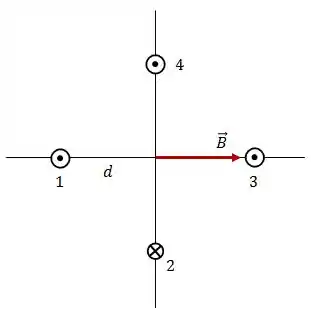
Passo 2
Para que valor de o fio 1 deve ser deslocado sobre o eixo para que o campo sofra uma rotação de no sentido anti-horário?
Antes de começar, vamos defini como sendo a componente em do campo magnético total e como sendo a componente em do campo magnético total. Onde:
Nesse caso, como não vamos mexer com os fio 2 e 4, será dado por:
Além disso, como não vamos mexer com o fio 3:
Continuando...
Agora, para que haja uma rotação de no sentido anti-horário, é necessário que:
Vamos reorganizando esse cara até acharmos o que estamos procurando:
Substituindo as expressões dos campos magnéticos, teremos:
Simplificando os termos:
Onde , finalmente:
SE LIGA!!!!!!!
Aqui tem uma pegadinha... o problema pergunta para que valor de o fio 1 deve ser deslocado. Assim, como ele deve ficar a da origem, ele deve ser deslocado para a posição:
Passo 3
Com o fio 1 na nova posição, para que valor de o fio 3 deve ser deslocado sobre o eixo para que o campo volta à orientação inicial?
Para que volte à orientação inicial, o campo magnético deve cancelar o campo magnético . Isso só vai acontecer se os dois estiverem à mesma distância da origem.
Assim, o fio 3 deve ser deslocado para a posição:
Resposta