Quatro partículas pontuais de cargas se movem com velocidades e , com . Num dado instante, as partículas ocupam os vértices de um quadrado de lado , no plano , como mostrado na figura abaixo.
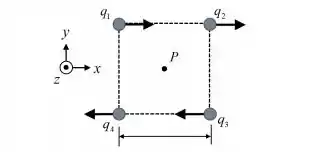
Quais são, respectivamente, o sentido do campo magnético produzido pelas quatro partículas no ponto , localizado no centro do quadrado, e a razão entre os módulos de e o módulo do campo magnético , produzido pela partícula também no ponto ?
(a)
(b)
(c)
(d)
(e) A soma do campo produzido pelas quatro partículas se anula.
Passo 1
Vamos usar a regra da mão direita da seguinte maneira: com o polegar no sentido da corrente, deve-se abraçar o “fio”, lembrando que o sentido convencionado à corrente é a movimentação de cargas positivas. Os demais dedos fazem a direção do campo magnético.
Como as partículas possuem mesma carga e mesma velocidade, exercerão o mesmo campo magnético , em módulo, no ponto . Pela regra da mão direita, as partículas da aresta horizontal superior exercerão um campo no sentido negativo de , assim como as partículas da aresta horizontal inferior, logo, o campo resultante no ponto terá módulo e seu sentido será , assim:
.
Resposta
(a)