UFU, Sem Campus, Eletromagnetismo, Testes de Eletromagnetismo 2 - Teste 1 - Leis de Conservação - 2023.1, Questão 1a
1. Considere um condutor cilíndrico de raio , comprimento e condutividade atravessado por uma corrente estacionária . Lembrando que a densidade de corrente pode ser escrita como , determine:
(a) O campo elétrico e magnético dentro e fora do cilindro.
Passo 1
Iae, como vai? Essa questão está difícil, né? Fique tranquilo que vamos tentar te ajudar. 😎👍
Nesse problema temos que obter o campo magnético e elétrico dentro e fora de um cilindro condutor de raio , comprimento e condutividade atravessado por uma corrente estacionária .
E agora? Como fazemos isso? 🤔
Se a corrente é estacionaria, ela não gera acúmulo de cargas no interior do condutor. Então para calcular o seu campo elétrico, temos que obter a diferença de potencial gerado pelo condutor já que não foi dito que sua condutividade é infinita...
Já o campo magnético no exterior do condutor pode ser obtido a partir da lei de Biot-Savart dada por
Já no interior, temos que aplicar a lei de Ampere, onde o campo diminui linearmente conforme diminui com relação a .
Sacou? Bora continuar! 😉
Passo 2
Vamos desenhar a situação do problema...
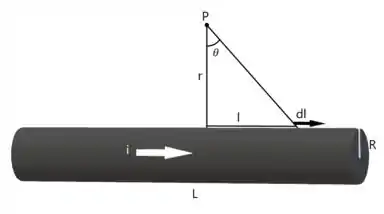
Pela equação de Biot-Savart, podemos definir o campo magnético fora do condutor como
No caso de um fio retilíneo como no nosso caso, podemos decorar que o resultado dessa integral complicadíssima resulta em simplesmente
Substituindo no nosso campo magnético, temos
Analisando , temos que pela lei dos senos
Já para , temos
Tranquilo até aqui? 😬
Passo 3
Substituindo esses resultados no nosso problema...
Portanto...
Agora, como nosso condutor conduz uma corrente estacionaria e uniforme, o campo magnético dentro dele reduz linearmente em relação a segundo a lei de Ampere, ou seja...
Bacana, não é? 😐
Passo 4
Com relação ao campo elétrico, sabemos que dentro de um condutor não há campo, então podemos afirmar que
Já no lado de fora do condutor, o movimento de cargas gera um potencial elétrico nas extremidades do condutor já que ele possui uma condutividade ...
Pela lei de Ohm, podemos obter que
Assim, podemos relacionar o potencial com o campo elétrico a partir da equação
é dado pelo valor infinitesimal do comprimento do condutor, ou seja
Isolando e substituindo , vamos obter
E todos viveram felizes para sempre. Fim! 😉 Entendeu tudo? Responde Aí
