O arranjo mostrado na figura abaixo é composto por dois fios retilíneos infinitos, paralelos entre si. Os fios estão separados por uma distância e são perpendiculares ao plano -. Em cada fio passa uma corrente elétrica , apontando nos sentidos indicados na figura.
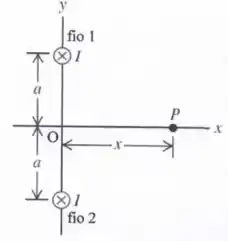
- Copie o diagrama da figura acima e nele desenhe os vetores campos magnéticos gerados pelo fio 1 ( ) e pelo fio 2 () no ponto que dista da origem .
- Calcule o módulo, direção e sentido do campo magnético total no ponto .
- Calcule para que valor de o módulo do campo magnético total é máximo.
- Determine o módulo do campo total quando .
Passo 1
a) O vetor campo magnético em um ponto qualquer produzido por uma corrente passando por um fio infinito é sempre perpendicular a esse ponto e seu módulo é dado por
sendo a distância do fio até o ponto . Além disso, é sempre perpendicular à reta que liga ao fio infinito.
Por isso, no caso da nossa questão aqui, o campo produzido pela corrente do fio em é perpendicular ao segmento de reta , e o campo produzido pelo fio em é perpendicular à reta , como mostra a figura abaixo. A direção e sentido desses campos são dados pela regra da mão direita.
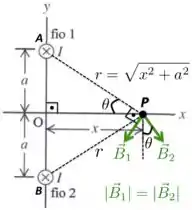
Além disso, é importante que a gente também identifique o ângulo que as retas e fazem com o eixo . Esse é também o ângulo que e fazem com a reta pontilhada vertical da figura.
Como as correntes que passam nos dois fios são iguais a e estão à mesma distância do ponto , então temos que:
Passo 2
b) Olhando para os vetores e da figura acima, vemos que ambos têm componentes ao longo das direções e . Na direção , as componentes desses vetores têm mesma direção, mesmo módulo (conforme vimos no Passo 1), mas sentidos opostos e, por essa razão, se cancelam.
Basta, portanto, que a gente tome apenas as componentes deles na direção , o que vai dar um módulo para campo resultante no ponto igual a:
em que usamos o fato de que os módulos dos campos produzidos pelas correntes são iguais.
Agora, precisamos ver como ficam e em termos das quantidades dados na figura do problema. Olhando para o triângulo retângulo da figura, temos que:
Substituindo isso na expressão para o módulo do campo resultante acima, obtemos que o vetor pode escrito como
Passo 3
c) Para sabermos qual valor dá o máximo para o campo, precisamos derivar o módulo do campo magnético e igualar a zero. Quando a gente faz isso, vamos ter que
Para que a derivada seja zero, o termo entre parênteses deve ser igual a zero:
que, tomando apenas a solução positiva, já que o ponto está do lado positivo do eixo , teremos
que maximiza o valor do módulo do campo magnético e seu valor será
Passo 4
d) Para ver como fica esse limtie, vamos reorganizar a expressão que obtivemos no final do Passo 2 da seguinte forma:
Se a gente faz nessa última expressão, vamos ter que
que seria o campo produzido no ponto que está muito distante dos dois fios infinitos. Repare que esse campo resultante no ponto é idêntico àquele que seria produzido por uma corrente de intensidade que passa num fio infinito que está a uma distância de ,
Nesse caso, o ponto está tão distante dos dois fios (), que é como se “ele visse”, a uma distância dele, um único fio infinito na origem conduzindo uma corrente que está entrando no plano da página.
Resposta
- Ver figura Passo 1 ;