UFJF – Física 3 – AV1 – 2014.1 – Questão 1a
Três cargas pontuais se encontram nos vértices de um triângulo equilátero de lado . O centro do triângulo está na origem de um sistema de coordenadas cartesianas e o plano do triângulo fica no plano . Uma das cargas está no eixo as outras simetricamente nos quadrantes III e IV, como mostra a figura. A carga no eixo assim como a carga no quadrante IV tem o valor e a carga no quadrante IV tem o valor .
(a) Calcule o valor do campo elétrico na origem de coordenadas. Escreva o seu resultado de forma vetorial usando a base .
Passo 1
Eaee!!! Belezinha? Bom... a questão nos dá três cargas pontuais onde elas se situam em cada ponta de um triângulo equilátero (que possui lados iguais).
A questão nos pede para calcularmos o campo elétrico no centro do triângulo.
Mas e aí? Como podemos fazer isso? Uma dica é usarmos a simetria do sistema para poder calcular!!
Não entendeu? Então bora junto aqui!!
Passo 2
Bom... observando os campos elétricos gerados por cada uma das cargas no centro do triângulo, temos:
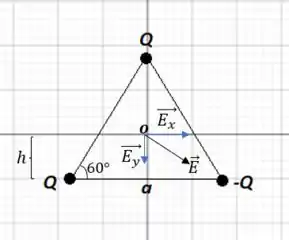
Onde é o centro do triângulo e é a altura do centro do triângulo até a base.
Obs: cargas positivas geram campo de afastamento e cargas negativas, de aproximação.
Passo 3
Sendo o ponto central do triângulo equilátero, sabe-se que a distância de um dos vértices até este ponto equivale a da altura do triângulo.
Sendo assim, a distância de cada vértice ao ponto é de:
Passo 4
Dessa forma, sabendo que o campo elétrico é dado por:
Onde é a constante eletrostática, temos:
Passo 5
Analisando a simetria dos campos, temos:
- No eixo :
- No eixo :
- No eixo não há campo elétrico resultante, portanto:
Passo 6
Dessa forma, o campo elétrico resultante tem a seguinte forma:
Entendeu direitinho? Responde aee ;)
