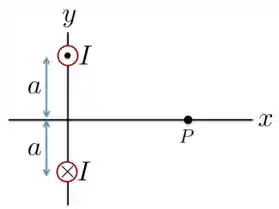
A Figura abaixo representa o plano que corta perpendicularmente dois fios longos (infinitos) e paralelos que conduzem uma corrente , de mesmo módulo, porém de sentidos contrários.
- Copie o diagrama e desenhe os vetores para mostrar que o campo magnético de cada fio e campo resultante no ponto .
- Deduza uma expressão para o módulo do campo em qualquer ponto do eixo em termos da coordenada do ponto. Qual é a direção e o sentido de ?
- Para qual valor de o módulo de atinge seu valor máximo?
- Qual é o módulo de quando ?
Passo 1
a) Na Figura abaixo, o fio de cima chamamos de e o debaixo de . O campo produzido por eles, e , respectivamente, são perpendiculares às linhas tracejadas de comprimento .
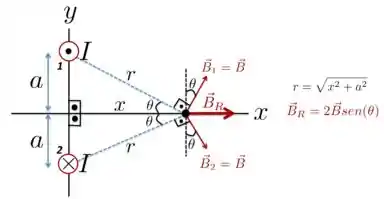
O campo magnético resultante no ponto é dado por
sendo que tem módulo
Passo 2
b) Da Figura acima, vemos que o vetor campo magnético resultante estará ao longo do eixo e terá módulo dado por
em que utilizamos, a partir da Figura acima, que
Passo 3
c) Se derivamos com relação a o módulo do vetor campo magnético resultante, chegamos a
Portanto, o campo magnético resultante é máximo em .
Passo 4
d) Se , então o campo magnético resultante é
Resposta
- Desenho da Figura ;
- é máximo em