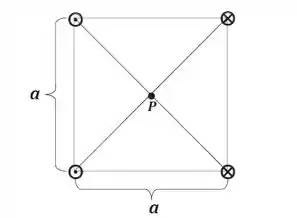
Quatro longos fios são dispostos ortogonalmente ao plano da página, como mostra a figura abaixo, sendo cada um deles percorrido, no sentido indicado, por uma corrente . Determine o vetor resultante no centro do quadrado.
Passo 1
Primeiramente, quando ele diz “longos fios”, ele quer dizer infinito. Agora, temos que lembrar que o módulo do campo magnético produzido por uma corrente transportada em um fio condutor infinito é:
Sendo R, a distância do ponto P até o fio.
Passo 2
Feito isso, nós vamos utilizar a regra da mão direita (como em todos os exercícios haha) em cada um dos fios.
Sejam as correntes 1, 2, 3 e 4, conforme a figura abaixo, nósteremos os respectivos campos magnéticos , . Em todos os outros pontos a intereção das 4 correntes irá gerar um campo magnético nulo.
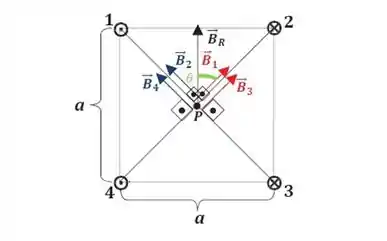
Lembrando que isso só ocorre pois todas as correntes possuem uma corrente de mesma intensidade, .
Passo 3
Por questões de simetria, todas as componentes horizontais irão se cancelar, sobrando apenas a componente vertical.
Temos que o módulo dos campos é dado por:
E como temos a soma dos quatro campos vamos ter que o campo magnético resultante é dado por:
E sabemos que o valor de é dado pela metade da diagonal do quadrado, ou seja:
Substituindo:
Agora só falta calcular a componente vertical do nosso campo magnético resultante:
Por se tratar de um quadrado, sabemos que o ângulo (em verde na figura) é de 45º.
Sendo assim, temos: