Dois fios muito longos dispostos paralelamente transportam a mesma intensidade de corrente e se repelem com uma força por unidade de comprimento de módulo . Se as correntes nos dois fios têm seus valores dobrados e a distância de separação entre os fios é triplicada, qual será o valor da intensidade da força por unidade de comprimento?
Passo 1
POW! Vamos começar esse problema falando um pouco sobre a força que está repelindo os dois fios, pode ser?
Para isso a gente vai imaginar dois fios longos que vou chamar de fio e fio , separados por uma distância e que a gente está aplicando correntes...

POW! Como tem corrente passando, vai ter campo magnético, certo? Então a corrente de produz um campo magnético em todos os pontos em especial em cima do fio e vice versa. Tem-se campo e tem corrente, então tem força !
Passo 2
O módulo da força que a corrente em faz em e vice e versa, , pode ser sempre calculada pela fórmula
é o módulo do campo da corrente onde o fio está e é o ângulo entre o vetor e o deslocamento da corrente.
O é todo o comprimento do fio. Como queremos calcular a quantidade de força por metro nesse cabo, podemos pegar a força total e dividir pelo comprimento do fio:
Agora, me diz aí, qual é a direção do vetor ?
Pela regra da mão direita...
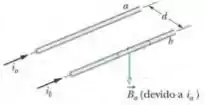
E cara, olha que maneiro: o deslocamento da corrente acontece exatamente a do campo magnético, de modo que...
Passo 3
O módulo de vai ser (considerando os fios longos):
Onde é a distância entre os fios. Então...
Passo 4
BELEZINHA! Agora que conhecemos a cara da força , vamos voltar para o nosso problema!
No nosso enunciado, ele disse que ambos os fios transportam a mesma corrente ...
E que em um determinado momento a corrente duplica e a distância triplica...
Resposta
LETRA D.