Halliday - Vol. 3 – 9º edição – Capítulo 29 – Seção 2 – Exercício 23
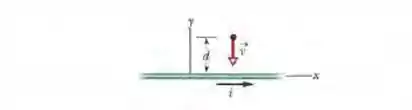
(Capítulo 29.2 – Exercício 23) A figura 29-50 mostra um próton que se move com velocidade em direção a um fio retilíneo longo que conduz uma corrente . No instante mostrado, a distância entre o próton e o fio é . Em termos dos vetores unitários, qual é a força magnética a que o próton está submetido?
Passo 1
Faaaala!
Gente, aqui é o seguinte: temos que achar o vetor força magnética, que será dado por:
Onde por se tratar de um próton.
A gente já tem a velocidade do próton . Então, nos resta saber o comportamento de .
Para isso, vamos usar a regra da mão direita na corrente! Colocando o polegar na direção de , quando formos girar nossos outros 4 dedos da mão, perceberemos que tem esse comportamento:
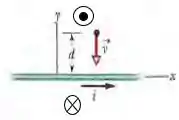
Então, olhando para o lado do próton, vemos que está saindo da tela. Logo, dizemos que ele está no sentido de . E o módulo desse vetor?? Lembra da fórmula para o campo magnético de um fio retilíneo? Calma, eu te lembro aqui:
Esse é o módulo do nosso campo, então, para ter o vetor, é só juntar as duas informações:
Tranquilo?
Passo 2
Assim, a força magnética é dada por:
Como, de acordo com o enunciado, , temos:
Como (podemos ver isso pela regra da mão direita também):
Substituindo os outros valores:
Arrasamos!
Resposta
A força magnética é igual a: