Considere um fio longo, percorrido por uma corrente com dois trechos retilíneos e um trecho de semicircunferência de raio com centro no ponto , conforme mostra a figura abaixo. O ponto fica a meio caminho dos dois trechos retilíneos e a uma distância muito grande da semicircunferência, de modo que para ele os dois trechos retilíneos podem ser considerados infinitos.
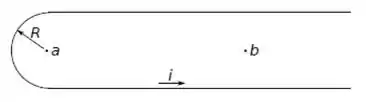
a) Calcule o módulo e o sentido do campo magnético no ponto .
b) Calcule o módulo e o sentido do campo magnético no ponto .
Passo 1
a) Pra calcularmos o campo magnético no ponto a, usamos o campo do fio semi-infinito, vamos ter isso:
Como temos o comprimento da metade de uma circunferência,
Então
Passo 2
b) No ponto b vamos usar o campo gerado pela linha de cima + o campo gerado pela linha de baixo:
Resposta
a)
b)