USP; Sem campus; Álgebra Linear 1; P1; 2022; Questão 12
Sejam pontos que não pertençam a uma mesma reta e considere o vetor
Seja o ponto tal que o vetor seja paralelo a e tal que seja paralelo
a . Assinale a alternativa correta:
Passo 1
Fala pessoal, tudo beleza? Vamos para mais uma questão de Algelin. Nosso objetivo é verificar qual relação entre , e está correta nas alternativas. Para isso, o enunciado nos informa que
pontos que não pertençam a uma mesma reta e considere o vetor
Seja o ponto tal que o vetor seja paralelo a e tal que seja paralelo
a .
Bem, vamos começar a desmembrar essas informações para resolver mais uma questão!!!!
Passo 2
Bem, temos as seguintes informações do enunciado.
pontos que não pertençam a uma mesma reta e considere o vetor
Seja o ponto tal que o vetor seja paralelo a e tal que seja paralelo
a .
Começando com o fato que pontos que não pertençam a uma mesma. O que isso quer dizer? Ora se eles são não colineares, então os vetores e são LI, que nem no desenho abaixo.
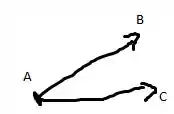
E o que podemos dizer sobre as informações a seguir?
o ponto tal que o vetor seja paralelo a e tal que seja paralelo
a .
Bem se seja paralelo a , então temos que
Pois ambos os vetores começam do mesmo ponto. Mas podemos escrever esse vetor de outra forma, podemos fazer
Como ilustrado na figura abaixo
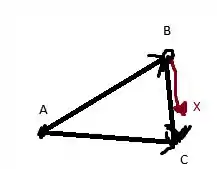
Mas Podemos escrever de outra forma, podemos fazer
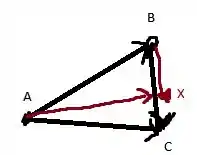
E de forma análoga, como é paralelo a , temos que
Passo 3
Agora podemos obter alguma relação entre , e . Como
e
e
Podemos juntar as duas primeiras igualdades para obter
Reescrevendo como e substituindo Temos:
Agora, como os vetores São LI, pois os pontos não pertencem a uma mesma reta. Temos que essa igualdade só será válida se
Somando as duas igualdades obtemos que:
e
Passo 4
Agora que sabemos que
e
Podemos substituir esse valor na igualdade
E obtemos que
Logo
Multiplicando os dois lados por temos:
Valor presente na alternativa
Prontinho pessoal!! Espero que os passos tenham ficado claros. Até a próxima questão e bons estudos!!!! 😊