UTFPR, sem campus, Geometria Analítica e Álgebra Linear, P1, 2018.1, questão 1b
Considere os vetores e
(b) e são ortogonais (perpendiculares)? Justifique.
Passo 1
Olá, genteeeee! Como estão por aí?
Nessa questão, devemos verificar se esses dois vetores do enunciado são ortogonais, que é o mesmo que serem perpendiculares. Isso significa que existe um ângulo de entre eles. Para saber se eles são ortogonais devemos calcular o produto escalar entre eles e o resultado deve ser nulo. Beleza?
Vamos lá resolver?
Passo 2
Bom, os vetores são: e .
O produto escalar é dado por:
Onde, , e são os elementos que compõem os vetores
Para que sejam ortogonais, temos que ter:
Vamos então substituir os valores e descobrir se o produto escalar é zero:
Logo,
Como o produto escalar não é nulo, os vetores não são ortogonais. Veja só, na figura abaixo, como fica a representação deles.
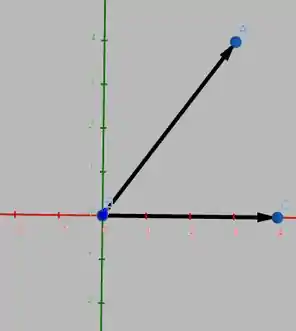
Viu que é simples? Até a próxima!
Resposta
Como o produto escalar não é nulo, os vetores não são ortogonais.