USP; Sem campus; Álgebra Linear 1; P1; 2022; Questão 10
Considere em um tetraedro regular de aresta unitária e seja o ponto da semirreta de origem passando por tal que
em que denota a distância entre os pontos . Temos que o produto
escalar dos vetores e é igual a:
Passo 1
Fala pessoal, tudo beleza? Vamos para mais uma questão de Algelin. Nosso objetivo é calcular o produto escalar dos vetores e . Onde
é um tetraedro de aresta unitária, cada aresta tem tamanho . E o ponto da semirreta de origem passando por tal que
Para fazer essa questão, vamos começar desenhando uma face do nosso tetraedro.
Passo 2
Vamos analisar a face abaixo
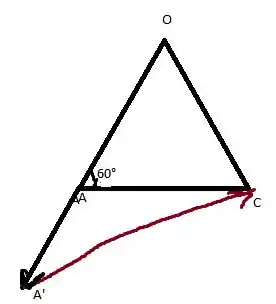
Agora fica mais fácil de visualizar que podemos escrever como:
Mas o enunciado diz que
E que pertence à mesma reta que . Ou seja, podemos escrever
Dessa forma, como
Podemos reescrever
Como
Passo 3
Agora que sabemos que
Podemos retomar a imagem e observar que o ângulo entre as arestas é de uma vez que o tetraedro é regular (tem todos as arestas iguais). Dessa forma, como
E as arestas tem tamanho então:
Pela linearidade do produto interno
Ou seja,
Valor presente na alternativa
Prontinho pessoal!! Espero que os passos tenham ficado claros. Até a próxima questão e bons estudos!!!! 😊