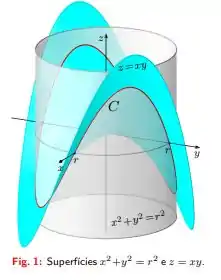
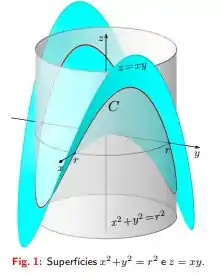
Seja a curva fechada dada pela interseção das superfícies de equações cartesianas e (Fig. 1).
Dê uma parametrização para a curva .
Passo 1
Eaew, tudo certinho contigo?
Temos uma curva obtida pela interseção entre as superfícies e , a interseção ocorre como na figura
Nesta alternativa precisamos encontrar uma parametrização para a curva! Então, vamos ver que expressão obtemos quando fazemos a interseção das expressões! Saca só!
Passo 2
Note que podemos escolher a seguinte parametrização para o cilindro como
e ,
Mas isso não é suficiente! Note que a interseção então requer que
Desta forma, a parametrização da curva como um todo é dada por
A primeira alternativa foi isso! Te vejo na próxima! Até já!