Interseção de Superfícies
A interseção das superfícies e é:
(a) uma parábola
(b) uma hipérbole
(c) uma elipse
(d) as superfícies não se interceptam
(e) uma circunferência
Passo 1
Esse passo não é obrigatório mas às vezes é bom poder visualizar as superfícies na hora de abordar a questão.
Essas superfícies não são muito complicadas, então a gente pode começar determinando o que elas são. Repare que elas têm equações bem parecidas! Identificamos algo na forma
que é a equação de uma esfera centrada em e de raio .
Então ambas têm raio 1, a primeira esfera tem , enquanto a segunda tem .
Ou seja, uma está centrada na origem e outra em , portanto é a mesma esfera deslocada pro lado. Show!
Passo 2
Agora vamos ao que interessa: a interseção das superfícies.
Basicamente queremos saber que figura geométrica formam os pontos que fazem parte tanto de uma superfície quanto da outra. E esses pontos, justamente por fazer parte das duas esferas, respeitam as equações das duas, certo?
Ótimo! Então pra esses pontos temos o sistema seguinte:
Ou seja:
Passo 3
Substituindo esse valor na primeira equação:
que é a equação de uma circunferência de raio .
Observação: substituindo na 2ª equação dá no mesmo, pois .
Olha como ficaram as esferas: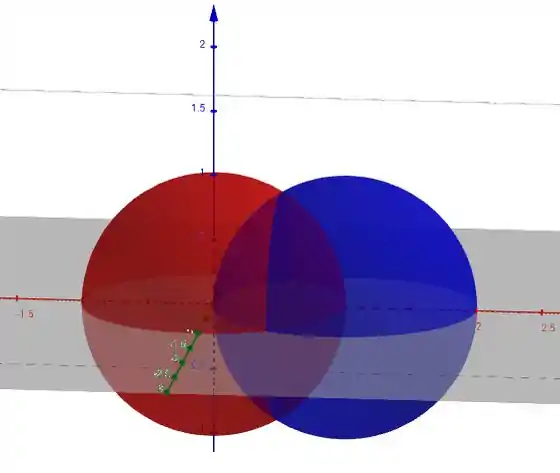
Resposta
Alternativa (e)