Considere as superfícies
E considere a superfície e a curva espacial .
a)Esboce a superfície e, sobre ela, desenhe a curva espacial .
b)Explicite uma parametrização da curva , determinando , e .
c) Seja a curva espacial obtida pela interseção da superfície com o plano , onde é a curva contida em e é a curva contida em .
- Desenhe a curva espacial sobre a superfície
- Identifique e como arcos de curvas planas conhecidas, denominando estas curvas e exibindo as suas equações cartesianas.
- Encontre os pontos e de interseção das curvas e
- Explicite as parametrizações de e , identificando os domínios destas.
Passo 1
a) E aí? Por onde vamos começar?
Quando temos superfícies, a maneira mais simples de esboçá-las, e que não costuma dar errado, é anular uma variável por vez. Assim, vemos a curva definida pelo corte do plano formado pelas outras duas variáveis que sobraram.
Fazendo isso para , temos:
Anulando ,
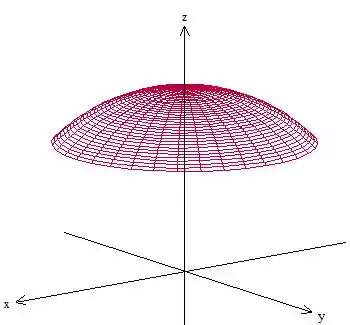
Essa curva é uma circunferência de raio , centrada na origem, no plano . E olha que legal, se anularmos as outras duas variáveis, e , uma de cada vez, teremos:
Que são outras duas circunferências, de mesmo raio , nos planos e , respectivamente. Com essas três curvas, podemos perceber que é uma esfera!
Mas atenção, como é maior do que , não é a esfera toda, mas apenas a parte da esfera a partir de :
Passo 2
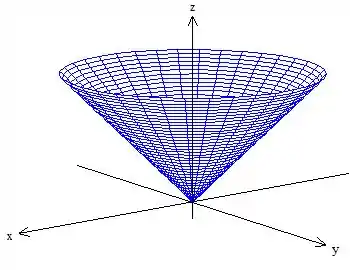
Agora vejamos que superfície é essa .
Essa é a equação do cone circular que já vimos na parte de superfícies.
Mas aqui tem um detalhe, ele quer que vá de à
Passo 3
Show, agora que temos as duas superfícies, vamos encaixá-las (o que dá certinho) e a vamos pensar na curva .
Bom, para encontrar a curva , precisamos isolar uma variável de uma das superfícies e jogar na outra equação. É mais conveniente pegar o do cone (que já está isolado) e jogar na equação da esfera:
Se pegarmos esse e jogar na esfera:
Temos:
E temos uma circunferência de raio centrada no eixo . Para saber em que altura ela se encontra, só jogar que em qualquer uma das equações, da esfera ou do cone (pois essa curva pertence a ambos):
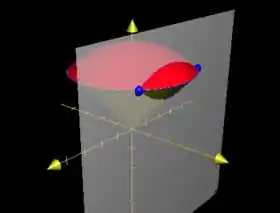
Ou seja, encontramos que a circunferência do passo anterior está em ! Então, como no spoiler que dei, provamos que realmente essa circunferência está “flutuando” onde termina uma superfície e começa a outra. É tipo uma casquinha de sorvete, você só vê parte da bola ;)
O desenho das superfícies juntas, com a curva de interseção fica assim:
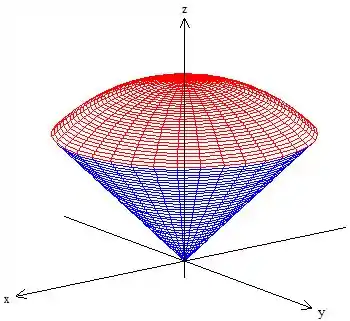
É tipo uma casquinha de sorvete :D
Passo 4
b) Essa foi dada de presente! Só precisamos pegar a curva que acabamos de encontrar e parametrizá-la!
Isso é uma circunferência, sabemos que a parametrização de uma circunferência é sempre com e . Como ela tem o eixo passando certinho pelo meio, estando deslocada apenas em no sentido positivo desse eixo, acrescentamos esse valor constante para a coordenada na nossa parametrização:
Como ela está em , e seu raio vale ,
E temos variando entre e , para fechar a circunferência completa :D
Passo 5
c.1) Essa é a hora que você pensa: AEEE!! Cheguei na última letra! Só que não. A letra parece que vai render mais passos que a e juntas D: Essa parada tá indo de até ...
Partiu destruir essa questão, e é agora. Primeiro ele pede pra desenhar a curva . Pelo enunciado, é a borda do nosso sorvete fatiado. Pra ficar mais claro, peguemos o desenho anterior e acrescentemos esse plano:
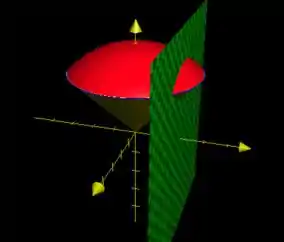
Show, isso é suficiente para a primeira parte ;)
Passo 6
c.2) Agora que temos a curva , que tem um pedaço na esfera e outro pedaço no cone, precisamos descobrir o que esses arcos são na verdade. Quando ele fala “curvas conhecidas”, é pra dizer se esse arco representa um pedaço de parábola, circunferência, reta, hipérbole, enfim, alguma curva que tenhamos ouvido falar em algum dia das nossas vidas.
Vamos chamar de o pedaço de que pertence à esfera, beleza? Pra o encontrarmos, temos que fazer a interseção do plano que fatiou , que é a própria esfera. Como o plano é , só colocar esse valor para na equação da ! O do plano meio que já “está isolado”:
Opa, encontramos uma circunferência de raio , centrada em ! Apenas ilustrando, ela é a curva de cima, que pertence à calota vermelha. A curva que está na parte do cone, é a ! Vamos ver quem ela é?
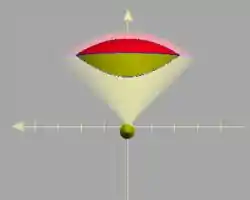
Passo 7
Vamos chamar de a parte de que pertence ao cone. Trocando por quando aparecer:
E que curva é essa? É uma hipérbole! Sabemos disso por que temos duas variáveis elevadas ao quadrado, subtraídas uma da outra, igualadas a uma constante. Legal né!? Não? Tá, desculpa XD
Passo 8
c.3)Para saber os pontos onde as curvas se interceptam, isolamos uma variável delas e substituímos na equação da outra, como sempre fazemos. Se pegarmos a ,
Isolando o ,
Jogando esse valor em ,
Tá, e o que isso significa? Significa que temos duas possibilidades para a coordenada , uma para cada ponto. Se você olhar de novo no desenho, ambas as curvas, e , estão sobre o plano , e qualquer coisa nesse plano sempre vai ter como valor da coordenada . Da mesma forma, nossa fatia é formada por duas curvas, e vemos que uma termina exatamente onde a outra começa, por que o cone e a esfera estão perfeitamente encaixados. Assim, a interseção entre e vai ter coordenada , pois ambas estão no mesmo plano, e coordenada , pois se interceptam na altura onde termina o cone e começa o pedaço de esfera!
Depois dessa filosofada toda, nossos pontos são e :D
Aqui os dois pontinhos no nosso sorvete:
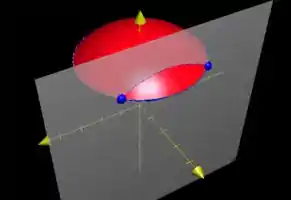
Passo 9
c.4)Agora sim!! Chegamos no último item!! Tao pedindo as parametrizações de e . E como faremos isso? Só isolar uma variável de cada uma e usar a outra como parâmetro! Olha só, para a teremos:
Usando como parâmetro, teremos a curva ! Lembrando que não temos a curva inteira, porque uma pedaço da fatia é um arco de circunferência e o outro de hipérbole, devemos dizer que , como encontramos no passo anterior ;)
Fazendo a mesma coisa para , teremos:
Usando como parâmetro, teremos a curva , com !
Resposta
a) 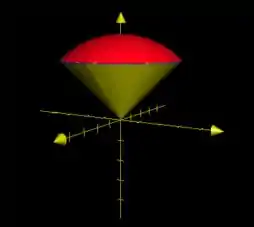
b),
c)