Seja a superfície de equação
b1) Estude a intersecção de com cada plano e com o plano . Esboce .
b2) Encontre uma parametrização para a intersecção de com o plano .
Passo 1
b1)
“Estude” soou muito como “encha linguiça a respeito de...” Mas vamos tentar fazer alguma coisa pra não zerar a questão né, nem que seja só um “brain-storm” aleatório XD
Ok, deram uma superfície:
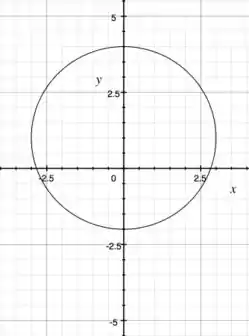
E disseram que tem uns planos fatiando-a, em . Para ficar mais fácil de visualizar, comecemos colocando uma constante real no lugar de ? Por exemplo, se fosse , teríamos:
Opa, essa é clássica, não? É uma circunferência no plano , paralelo ao , com centro em e .
Passo 2
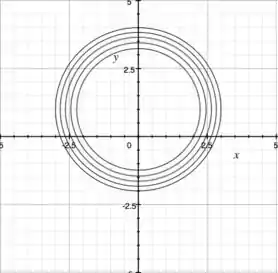
Show, mas e se fosse simplesmente ? Sabe, um número aleatório?
Opa, viu só? Vemos sempre, o examinador queira ou não, circunferências! Como está ao quadrado, não importa se ele é negativo ou positivo, sempre vai dar uma circunferência descolada em no sentido de . A única coisa que vai mudar é o raio, no caso, .
Passo 3
Agora que já “estudamos” os plano , acho eu, o suficiente, vamos partir pro plano e ver a curva que temos:
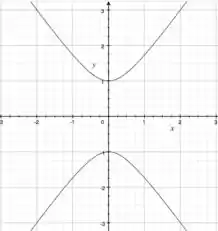
Substituindo por onde aparecer...
Pronto! Consegue ver o que encontramos? Temos uma hipérbole desenhada no plano paralelo ao :D
Passo 4
Depois disso tudo o que fizemos, fica mais intuitivo pensar em esboçar a superfície! Pense só, temos uma superfície, e sabemos a sua equação do “mundo tridimensional”, certo? Então, fatiamos ela por planos paralelos aos planos cartesianos, ou seja, por planos do tipo , , . Se o planos são , como no início da questão, então eles são paralelos ao plano , se são , são paralelos ao , e se são , são paralelos a .
Sem mais enrolação, vamos analisar o que já fizemos? Se fatiamos a superfície com planos , paralelos a , encontramos circunferências, certo? Lembra que sempre encontrávamos elas, não importando o valor de ? Se fatiamos por planos , encontramos hipérboles. Analogamente, se tivéssemos anulado o , teríamos encontrado hipérboles, pois teríamos e elevados ao quadrado, sendo um subtraído do outro...
Juntando essas três informações, temos um hiperboloide de uma folha!


Viu a circunferência aí quando , deslocada em no sentido positivo de ? E não importa se é maior ou menor que nos planos ! Sempre fatiaremos circunferências!
Passo 5
b2)
Beleza, agora temos que fazer a interseção entre e . A maneira mais intuitiva é isolar o , né? Ele já está quase isolado... Aí depois substituímos na equação da superfície :D
Colocando na superfície:
O que acha da gente desenvolver esse ? Aí poderemos completar o quadrado, juntando com o que sobrou do lado esquerdo...
Completando o quadrado...
Dividindo por , pra sair a equação certinha de uma elipse:
Passo 6
Agora só precisamos parametrizar com coordenadas elípticas! Hahaha o nome é feio, mas é assim mesmo.
O pensamento é o seguinte: Temos dois termos ao quadrado, sendo somados e igualados a . Então, depois que fizermos nossa substituição, teremos que encontrar . Sacou?
No nosso caso, o primeiro termo é . Queremos que vire apenas , beleza? Então:
Então dizemos que !
E o ? Queremos que vire , certo? Então:
Então,
Viu como é simples? Depois, de tanto fazer isso, você vai fazer sem pensar, vai sair naturalmente :)
E então a parametrização da curva é:
Resposta
b1) 
b2)