Considere a quádrica de equação
- Essa quádrica é um hiperboloide que corta o plano
- Uma parametrização da interseção da quádrica com o plano é
- Uma parametrização da interseção do plano com a porção da quádrica no semi espaço é
- Todas as afirmações são verdadeiras
- As afirmações I e III são verdadeiras
- As afirmações II e III são verdadeiras
- As afirmações I e III são falsas
- As afirmações II e III são falsas
Passo 1
Vamos analisar cada uma das alternativas.
“Essa quádrica é um hiperboloide que corta o plano ”
Antes de mais nada, vamos lembrar rapidamente como é a equação geral de um hiperboloide.
De uma folha:
De duas folhas:
Agora vamos olhar pra equação da nossa quádrica:
Como temos duas variáveis com sinal negativo, já podemos perceber que isso seria um hiperboloide de duas folhas. Beleza.
Arrumando um pouquinho melhor isso, podemos completar quadrados em :
Se repararmos, a equação geral do hiperboloide tem o lado direito igual a 1, então vamos dividir os dois lados por :
Trata-se portanto de um hiperboloide de duas folhas que está ao longo do eixo , com centro em .
Como ele tem uma cara mais ou menos como essa aqui:
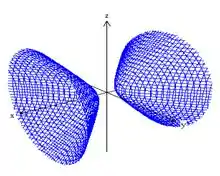
Ele não pode estar cortando o plano .
Passo 2
“Uma parametrização da interseção da quádrica com o plano é ”
Vamos substituir na equação da quádrica:
Isso é a equação de uma circunferência no plano com centro na origem e raio .
E a parametrização da circunferência é, de fato
Mas, isso é só a projeção da curva no plano , né.
Na real a curva tá no espaço e a coordenada dela vale , Porque afinal essa curva veio da interseção da quádrica com o plano , beleza?
Então a parametrização da curva de interseção é, de fato
Afirmativa II é verdadeira!!
Passo 3
“Uma parametrização da interseção do plano com a porção da quádrica no semi espaço é ”
Agora vamos substituir na equação da quádrica:
Completando quadrados em :
Dividindo ambos os lados por :
E isso é uma hipérbole no plano , com centro em .
E a parametrização da hipérbole é, de fato
Mas, isso é só a projeção da curva no plano , né.
Na real, do mesmo modo que vimos antes, a curva tá no espaço e a coordenada dela vale , Porque afinal essa curva veio da interseção da quádrica com o plano , certo?
Então a parametrização da curva de interseção é, de fato
Então a afirmativa III também é verdadeira!!
Resposta
Letra