Calcular o módulo dos vetores e , sabendo que e o ângulo entre e é de .
Passo 1
Esse problema nos dá os seguintes dados:
Pede para calcularmos o módulo dos vetores e .
Passo 2
Não sei nem por onde começar, ferrou!!!

Calma, tem alguns conhecimentos prévios que são fundamentais. Esse, é aquele tipo de exercício que sabemos resolver se já o vimos uma vez na vida hehe.

Lembra da Regra dos Cossenos, lá do Vestibular??? Se não se lembrar, relaxa aí!!
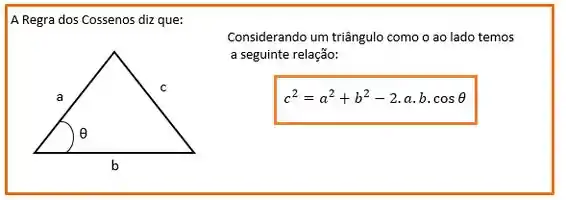
Repara que o lado c é o lado que está oposto ao ângulo , e os lados a e b são os que aparecem entre esse ângulo!
Passo 3
Olhando a figura acima podemos fazer uma associação entre os lados do triângulo com vetores.
Ué, como assim? O lado é um tamanho e o vetor é uma seta!
Isso mesmo, mas você pode ver os lados como se fossem o módulo do vetor, já que o módulo representa o tamanho do vetor.
Assim, com os dados do problema temos que:
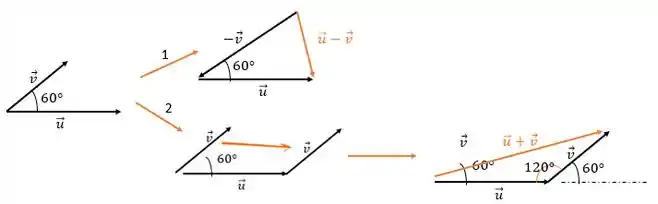
A setinha 1 indica o caso do vetor . Se você não lembra de como faz essa diferença de vetores dá uma olhadinha rápida lá no tópico de Introdução aos Vetores =)
O problema nos pede para calcular o módulo desse vetor .
Para isso, vamos utilizar a Regra dos Cossenos que vimos no Passo 2.
Aplicando essa regra no triângulo da setinha 1, vamos ter:
Como sabemos que módulo indica o comprimento do vetor, então o sentido do vetor, ou seja, ele ser ou não altera o seu módulo, apenas o sentido.
Com os dados fornecidos no enunciado chegamos que:
Assim,
Passo 4
Para finalizar, consideraremos a setinha 2 que indica o caso . De novo, se você não lembra de como faz essa soma de vetores dá uma olhadinha rápida lá no tópico de Introdução aos Vetores =)
O passo a passo é o mesmo do caso , só temos que nos atentar que agora o ângulo a ser considerado não é mais e sim como mostra a figura, já que o corresponde ao ângulo oposto a .
Assim,