USP, Sem Campus, Álgebra Linear 1, P2 - 2017, Questão 12
Considere no espaço um cubo cujos vértices são , em que e são faces desse cubo, como ilustrado na figura abaixo:
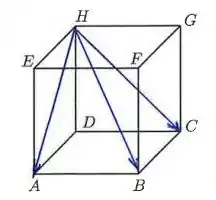
Considere também os seguintes sistemas de coordenadas em :
Se for o ponto cujos coordenadas no sistema são , então as coordenadas de no sistema serão:
a)
b)
c)
d)
e)
Passo 1
Fala aí pessoal, tudo certinho?
Nessa questão temos um tipo de sistema de coordenadas um pouco diferente. Nos é dado um cubo, e é falado que existem dois sistemas de coordenadas em . Vou mostrar pra vocês como funciona.
Para , por exemplo, foi falado que:
Então, se a gente pegar um ponto qualquer que é dado por no sistema de coordenadas , significa que:
Entenderam?
Daí, o enunciado fala que em um ponto é dado por e nos pergunta quais as coordenadas de no sistema de coordenadas . Sacou?
Para responder essa pergunta precisamos primeiro identificar as relações entre e
. Nesse processo é fundamental utilizar os paralelismos entre vetores do cubo.
Depois, podemos utilizar que em para chegar na sua relação em . Tranquilo?
Vamo nessa!
Passo 2
Então, pra começar precisamos identificar as relações entre e .
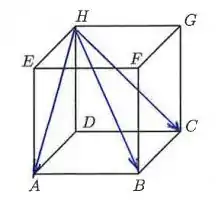
Analisando o nosso cubo, vemos que:
É isso que queremos fazer! Encontrar uma relação pra cada vetor de em função dos vetores
Agora vamos para .
É um pouco difícil perceber logo de cara uma relação para , mas observando que , e que além de serem paralelos possuem o mesmo comprimento (ou seja, ), podemos escrever que:
Perfeito!
Por fim, precisamos encontrar uma relação pra .
Aqui fica um pouquinho mais difícil, então vamos com calma. Usando o mesmo raciocínio de antes, podemos escrever que:
Mas, quem é
Olhando direitinho, vemos que é paralelo a , porém aponta no sentido contrário. Assim:
Substituindo o valor de que encontramos anteriormente na nossa expressão para , vem que:
Ou seja:
Excelente! Revisando o que encontramos aqui, temos:
Muito bom!
Passo 3
Agora vamos usar a informação de que, na base , .
Mas, . Logo:
Usando a relação que encontramos no passo anterior:
Temos:
Massa! Estamos quase lá. Para escrever na base precisamos chegar em uma expressão do tipo:
E, até agora já temos:
Uma sacada bem legal é reescrever como:
Só que é paralelo a mas em sentido oposto. Ou seja:
Assim:
Substituindo de volta na expressão para , temos:
Lembrando que:
Temos:
Olha aí que bonito! É exatamente onde queríamos chegar. Daí, podemos afirmar que em vale:
(é só pegar os coeficientes que multiplicam e .
Prontinho gente! É isso.
Espero que vocês tenham gostado, até a próxima 😉
Resposta
Letra b)