Sabe-se que é um vértice de um quadrado que possui diagonal contida na reta r: . Então é correto afirmar que existe um outro vértice do quadrado com a+b+c igual a:
Passo 1
Falaaaa, tranquilo??? Vamos começar essa questão reescrevendo essa reta r de uma forma mais fácil de enxergar.
Daqui tiramos que:
Veja que a questão não quis ser legal conosco, pois o ponto A não pertence à reta r. Caso contrário seria bem mais fácil.
Passo 2
Vamos fazer um desenho para ficar mais claro o que está acontecendo:
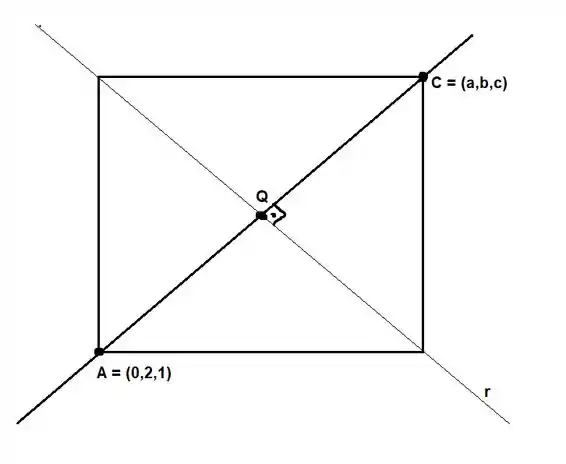
Só quero deixar bem claro que sei desenhar bem no papel, mas digitando fica sempre um desastre, sem julgamentos, por favor.
Mas enfim, superando a arte acima, vamos ao que nos interessa.
Veja que , logo, basta acharmos o valor de Q que resolvemos a questão
Passo 3
Como
Então
Além disso, , onde é paralelo a reta r.
Da equação parametrizada, tiramos que
Vamos agora fazer o produto escalar entre os 2 vetores perpendiculares citados:
Então , logo:
Como foi dito anteriormente
Como