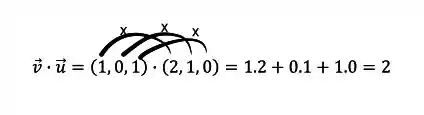Determine o valor do produto interno entre os vetores e .
Passo 1
E aí, vamos começar a esquentar os motores? Então, vamos nessa....
O enunciado pede para calcularmos o produto interno entre os vetores e . Então, aqui é importante ressaltar que já nos foi dado os vetores bonitinhos, com as coordenadas certas. Assim, não precisamos fazer nenhuma manipulação para encontrar os vetores, eles já nos foram dados, okay?
Passo 2
Bom, como vimos na teoria para achar o produto escalar entre dois vetores temos que multiplicar as coordenadas correspondentes uma a uma e depois somá-las, ou seja, devemos multiplicar a componente do vetor pela componente do vetor , e assim, para todas as demais coordenadas.
Assim,
Resposta
Exercícios de Livros Relacionados
Escreva cada combinação de vetores como um único vetor. P Q → + Q R → R P → + P S → Q S → - P S → R S → + S P → + P Q →
Ache um vetor que possui a mesma direção e o mesmo sentido que - 2,4 , 2, mas tem comprimento 6 .
Velocidades têm módulo, direção e sentido, sendo portanto vetores. O módulo de uma velocidade é chamado velocidade escalar. Suponha que esteja ventando na direção N 45 ° W a uma velocidade de 50 km/h.
Suponha que a e b sejam vetores não nulos, não paralelos e que c seja um vetor pertencente ao plano determinado por a e b . Dê um argumento geométrico para mostrar que c pode ser escrito como c = s a
Determine a + b , 2 a + 3 b , |a| e |a - b| . 18. a = 4 i + j , b = i - 2 j