Dados os vetores e e os pontos e , determinar o valor de tal que .
Passo 1
Esse exercício nos dá várias informações. Então, vamos com calma!! Primeiro, vamos retirar do problema tudo o que ele nos fornece de informação!!
Dados: Vetores Pontos
Pronto!! Já temos os dados separados. Bom, então o problema pede para determinarmos o valor de para que a expressão seja válida.
Passo 2
Nessa expressão, o que não temos é o vetor , pois só foi nos fornecido os pontos e . Assim, vamos primeiro encontrar o vetor .
Passo 3
Agora, podemos começar a resolver nossa expressão, começando pela soma.
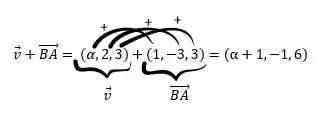
Por fim, realizamos o produto interno.
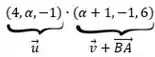
Como a questão quer que esse resultado seja igual a 5:
Resposta
Exercícios de Livros Relacionados
Escreva cada combinação de vetores como um único vetor. P Q → + Q R → R P → + P S → Q S → - P S → R S → + S P → + P Q →
Ache um vetor que possui a mesma direção e o mesmo sentido que - 2,4 , 2, mas tem comprimento 6 .
Velocidades têm módulo, direção e sentido, sendo portanto vetores. O módulo de uma velocidade é chamado velocidade escalar. Suponha que esteja ventando na direção N 45 ° W a uma velocidade de 50 km/h.
Suponha que a e b sejam vetores não nulos, não paralelos e que c seja um vetor pertencente ao plano determinado por a e b . Dê um argumento geométrico para mostrar que c pode ser escrito como c = s a
Determine a + b , 2 a + 3 b , |a| e |a - b| . 18. a = 4 i + j , b = i - 2 j